
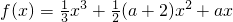 ,x∈R,a∈R.
,x∈R,a∈R.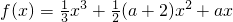 ,∴f′(x)=x2+(a+2)x+a.
,∴f′(x)=x2+(a+2)x+a.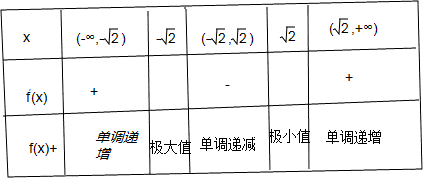
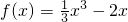 ,f′(x)=x2-2.
,f′(x)=x2-2.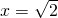 .
.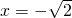 时,f(x)极大值=
时,f(x)极大值=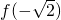 =
= ;
; 时,f(x)极小值=
时,f(x)极小值=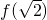 =
=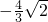 .
. 在区间(1,2)上恒成立.
在区间(1,2)上恒成立. ,则g′(x)=-
,则g′(x)=-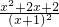 =-
=-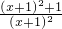 <0,
<0, .
.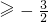 .
. 在区间(1,2)上恒成立?a≥
在区间(1,2)上恒成立?a≥ ,x∈(1,2),解出即可.
,x∈(1,2),解出即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:专项题 题型:解答题
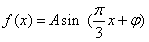 ,x∈R,A>0,
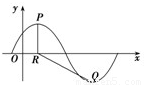
,x∈R,A>0,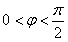 。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。
。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。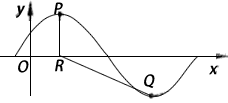
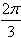 ,求A的值。
,求A的值。查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省永州市祁阳四中高三(上)段考数学试卷(文科)(解析版) 题型:解答题
 已知函数
已知函数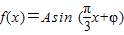 ,x∈R,A>0,
,x∈R,A>0,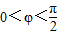 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).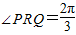 ,求A的值.
,求A的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省永州市祁阳四中高三(上)段考数学试卷(文科)(解析版) 题型:解答题
 已知函数
已知函数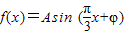 ,x∈R,A>0,
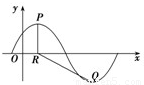
,x∈R,A>0,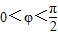 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).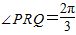 ,求A的值.
,求A的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省数学试卷双流市棠中外语学校高三(上)9月月考数学试卷(文科)(解析版) 题型:解答题
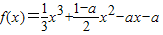 ,x∈R其中a>0.
,x∈R其中a>0.查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市源清中学高一(下)数学暑假作业(三角函数)(解析版) 题型:解答题
 已知函数
已知函数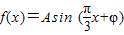 ,x∈R,A>0,
,x∈R,A>0,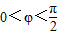 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).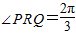 ,求A的值.
,求A的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com