练习册系列答案
相关习题
科目:高中数学
来源:2011届河北省石家庄市自强中学高三数学练习试卷5
题型:单选题
查看答案和解析>>
科目:高中数学
来源:2011-2012学年湖北省高三高考模拟理科数学试卷一
题型:解答题
查看答案和解析>>
科目:高中数学
来源:2011-2012学年安徽省东至县高三一模文科数学试卷
题型:解答题
已知函数 ,数列
,数列 满足
满足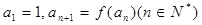
(1)证明 求数列
求数列 的通项公式;
的通项公式;
(2)记 ,求
,求 .
.
查看答案和解析>>
科目:高中数学
来源:河北省三河一中2011-2012学年高三上学期第二次月考(数学文)
题型:解答题
已知函数 ,数列
,数列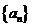 满足
满足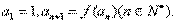
(1)求数列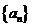 的通项公式;(2)记
的通项公式;(2)记 ,求
,求 .
.
查看答案和解析>>
科目:高中数学
来源:河北省三河一中2011-2012学年高三上学期第二次月考(数学理)
题型:解答题
已知函数 ,数列
,数列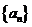 满足
满足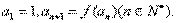
(1)求数列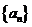 的通项公式;(2)记
的通项公式;(2)记 ,求
,求 .
.
查看答案和解析>>

![]() ,数列
,数列![]() 满足
满足![]()
![]() 时,不等式
时,不等式![]() 恒成立;
恒成立;![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]()