
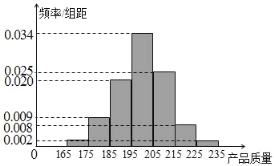
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取100件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
(165,175] | 3 |
(175,185] | 2 |
(185,195] | 21 |
(195,205] | 36 |
(205,215] | 24 |
(215,225] | 9 |
(225,235] | 5 |
(Ⅰ)根据乙流水线样本的频率分布直方图,求乙流水线样本质量的中位数(结果保留整数);
(Ⅱ)从甲流水线样本中质量在![]() 的产品中任取2件产品,求两件产品中恰有一件合格品的概率;
的产品中任取2件产品,求两件产品中恰有一件合格品的概率;
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅲ)由以上统计数据完成下面2×2列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
下面临界值表仅供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)不能在犯错误的概率不超过0.15的前提下,认为产品的包装合格与两条自动包装流水线的选择有关.
(Ⅲ)不能在犯错误的概率不超过0.15的前提下,认为产品的包装合格与两条自动包装流水线的选择有关.
【解析】
(Ⅰ)求出前三组的频率之和及前四组的频率之和,则可判断中位数在第四组,设其大小为![]() ,由
,由![]() 解得
解得![]() ;
;
(Ⅱ)甲流水线样本中质量在![]() 的产品共有5件,其中合格品有2件,设为
的产品共有5件,其中合格品有2件,设为![]() ;不合格品3件,设为
;不合格品3件,设为![]() ,再利用列举法以及古典概型概率公式可得;
,再利用列举法以及古典概型概率公式可得;
(Ⅲ)先得列联表,再根据表中数据,计算出观测值,结合临界值表可得.
(Ⅰ)因为前三组的频率之和![]()
前四组的频率之和![]()
所以中位数在第四组,设为![]()
由![]() ,解得
,解得![]() .
.
(Ⅱ)甲流水线样本中质量在![]() 的产品共有5件,其中合格品有2件,设为
的产品共有5件,其中合格品有2件,设为![]() ;不合格品3件,设为
;不合格品3件,设为![]()
从中任取2件的所有取法有![]() ,
,![]() 共10种,
共10种,
恰有一件合格品的取法有![]() 共6种,
共6种,
所以两件产品中恰有一件合格品的概率为![]() .
.
(Ⅲ)由乙流水线样本的频率分布直方图可知,合格品的个数为![]() ,
,
甲流水线 | 乙流水线 | 总计 | |
合格品 | 92 | 96 | 188 |
不合格品 | 8 | 4 | 12 |
总计 | 100 | 100 | 200 |
所以,2×2列联表是:
所以![]()
不能在犯错误的概率不超过0.15的前提下,认为产品的包装合格与两条自动包装流水线的选择有关.


科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若直线l:x+y=0与圆C交于A,B两点,求弦AB的长;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电子计算机诞生于20世纪中叶,是人类最伟大的技术发明之一.计算机利用二进制存储信息,其中最基本单位是“位(bit)”,1位只能存放2种不同的信息:0或l,分别通过电路的断或通实现.“字节(Byte)”是更大的存储单位,1Byte=8bit,因此1字节可存放从00000000(2)至11111111(2)共256种不同的信息.将这256个二进制数中,所有恰有相邻两位数是1其余各位数均是0的所有数相加,则计算结果用十进制表示为
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电子计算机诞生于20世纪中叶,是人类最伟大的技术发明之一.计算机利用二进制存储信息,其中最基本单位是“位(bit)”,1位只能存放2种不同的信息:0或l,分别通过电路的断或通实现.“字节(Byte)”是更大的存储单位,1Byte=8bit,因此1字节可存放从00000000(2)至11111111(2)共256种不同的信息.将这256个二进制数中,所有恰有相邻两位数是1其余各位数均是0的所有数相加,则计算结果用十进制表示为
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的矩形ABCD中,AB=![]() AD=2,点E为AD边上异于A,D两点的动点,且EF//AB,G为线段ED的中点,现沿EF将四边形CDEF折起,使得AE与CF的夹角为60°,连接BD,FD.
AD=2,点E为AD边上异于A,D两点的动点,且EF//AB,G为线段ED的中点,现沿EF将四边形CDEF折起,使得AE与CF的夹角为60°,连接BD,FD.
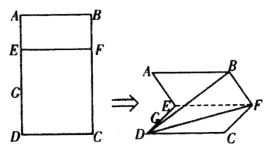
(1)探究:在线段EF上是否存在一点M,使得GM//平面BDF,若存在,说明点M的位置,若不存在,请说明理由;
(2)求三棱锥G—BDF的体积的最大值,并计算此时DE的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
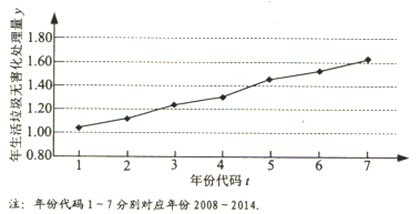
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)的左、右顶点分别为A1(﹣2,0),A2(2,0),右准线方程为x=4.过点A1的直线交椭圆C于x轴上方的点P,交椭圆C的右准线于点D.直线A2D与椭圆C的另一交点为G,直线OG与直线A1D交于点H.
(a>b>0)的左、右顶点分别为A1(﹣2,0),A2(2,0),右准线方程为x=4.过点A1的直线交椭圆C于x轴上方的点P,交椭圆C的右准线于点D.直线A2D与椭圆C的另一交点为G,直线OG与直线A1D交于点H.
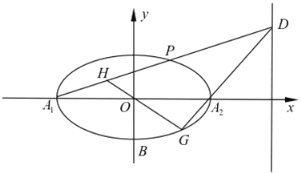
(1)求椭圆C的标准方程;
(2)若HG⊥A1D,试求直线A1D的方程;
(3)如果![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com