
【题目】如图所示的矩形ABCD中,AB=![]() AD=2,点E为AD边上异于A,D两点的动点,且EF//AB,G为线段ED的中点,现沿EF将四边形CDEF折起,使得AE与CF的夹角为60°,连接BD,FD.
AD=2,点E为AD边上异于A,D两点的动点,且EF//AB,G为线段ED的中点,现沿EF将四边形CDEF折起,使得AE与CF的夹角为60°,连接BD,FD.
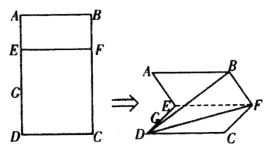
(1)探究:在线段EF上是否存在一点M,使得GM//平面BDF,若存在,说明点M的位置,若不存在,请说明理由;
(2)求三棱锥G—BDF的体积的最大值,并计算此时DE的长度.
【答案】(1)见解析;(2)![]() ,2
,2
【解析】
(1)取线段EF的中点M,得GM∥DF,由线面平行的判定定理可得GM∥平面BDF;(2)由题意可得AE与DE的夹角为60°,过D作DP垂直于AE交AE于P,可得DP为点D到平面ABFE的距离,设DE=x,则AE=BF=4﹣x,利用等积法写出三棱锥G﹣BDF的体积,再由基本不等式求最值,并求出DE的长度
(1)取线段EF的中点M,有GM∥平面BDF.
证明如下:如图所示,取线段EF的中点M,
∵G为线段ED的中点,M为线段EF的中点,
∴GM为△EDF的中位线,故GM∥DF,
又GM平面BDF,DF平面BDF,故GM∥平面BDF;
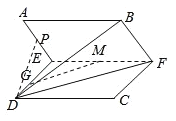
(2)∵CF∥DE,且AE与CF的夹角为60°,故AE与DE的夹角为60°,即![]() ,
,
过D作DP⊥AE交AE于P,
由已知得DE⊥EF,AE⊥EF,∴EF⊥平面AED,
EF⊥DP,又AE![]() EF=E,∴DP⊥平面AEFB,
EF=E,∴DP⊥平面AEFB,
即DP为点D到平面ABFE的距离,且![]() ,
,
设DE=x,则AE=BF=4﹣x,
由(1)知GM∥DF,
![]()
![]()
![]() ,
,
当且仅当4﹣x=x时等号成立,此时x=DE=2.
故三棱锥G﹣BDF的体积的最大值为![]() ,此时DE的长度为2.
,此时DE的长度为2.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】从某公司生产线生产的某种产品中抽取![]() 件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
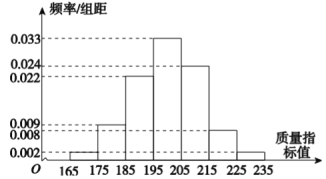
(Ⅰ)求这![]() 件产品质量指标的样本平均数
件产品质量指标的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)由直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)已知每件该产品的生产成本为![]() 元,每件合格品(质量指标值
元,每件合格品(质量指标值![]() )的定价为
)的定价为![]() 元;若为次品(质量指标值
元;若为次品(质量指标值![]() ),除了全额退款外且每件次品还须赔付客户
),除了全额退款外且每件次品还须赔付客户![]() 元。若该公司卖出
元。若该公司卖出![]() 件这种产品,记
件这种产品,记![]() 表示这件产品的利润,求
表示这件产品的利润,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]()
(1)试寻找一个等差数列![]() 和一个非负常数
和一个非负常数![]() ,使得等式
,使得等式![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,并说明你的理由;
恒成立,并说明你的理由;
(2)对于(1)中的等差数列![]() 和非负常数
和非负常数![]() ,试求
,试求![]() (
(![]() )的最大值.
)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
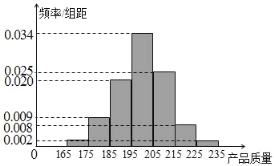
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取100件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
(165,175] | 3 |
(175,185] | 2 |
(185,195] | 21 |
(195,205] | 36 |
(205,215] | 24 |
(215,225] | 9 |
(225,235] | 5 |
(Ⅰ)根据乙流水线样本的频率分布直方图,求乙流水线样本质量的中位数(结果保留整数);
(Ⅱ)从甲流水线样本中质量在![]() 的产品中任取2件产品,求两件产品中恰有一件合格品的概率;
的产品中任取2件产品,求两件产品中恰有一件合格品的概率;
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅲ)由以上统计数据完成下面2×2列联表,能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
下面临界值表仅供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解社区群众体育活动的开展情况,拟采用分层抽样的方法从A,B,C三个行政区抽出6个社区进行调查.已知A,B,C行政区中分别有12,18,6个社区.
(1)求从A,B,C三个行政区中分别抽取的社区个数;
(2)若从抽得的6个社区中随机的抽取2个进行调查结果的对比,求抽取的2个社区中至少有一个来自A行政区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com