
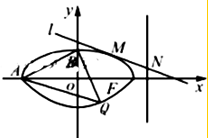
 (理科)如图所示的封闭曲线C由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和曲线C2:y=nx2-1(y<0)组成,已知曲线C1过点($\sqrt{3}$,$\frac{1}{2}$),离心率为$\frac{\sqrt{3}}{2}$,点A、B分别为曲线C与x轴、y轴的一个交点.
(理科)如图所示的封闭曲线C由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和曲线C2:y=nx2-1(y<0)组成,已知曲线C1过点($\sqrt{3}$,$\frac{1}{2}$),离心率为$\frac{\sqrt{3}}{2}$,点A、B分别为曲线C与x轴、y轴的一个交点.分析 (I)曲线C1过点($\sqrt{3}$,$\frac{1}{2}$),离心率为$\frac{\sqrt{3}}{2}$,可得$\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}$=1,$\frac{c}{a}=\frac{\sqrt{3}}{2}$,又a2=b2+c2,联立解得可得曲线C1的方程.可得A,代入曲线C2方程,即可得出方程.
(II)A(-2,0),B(0,1),利用截距式可得直线AB的方程.由题意可知:当曲线C2在点Q处的切线与直线AB平行时,△QAB的面积最大,设切线方程为:x-2y+t=0,可知:切线斜率为$\frac{1}{2}$,利用导数的几何意义可得切线的斜率,进而得出切点Q.代入切线方程可得t,利用平行线之间的距离公式可得:△QAB的AB边上的高h,即可得出面积的最大值.
(III)由题意可得:k≠0,F$(\sqrt{3},0)$,N$(-\frac{m}{k},0)$.设切点M(x0,y0),直线方程与椭圆方程联立化为:(1+4k2)x2+8kmx+4m2-4=0,又直线l与曲线C1相切于点M,可得△=0,即m2=4k2+1.利用根与系数的关系解出M.可得N,$\overrightarrow{FM}$,$\overrightarrow{FN}$,利用$\overrightarrow{FM}•\overrightarrow{FN}$=0,即可证明以MN为直径的圆过点F.
解答 (I)解:∵曲线C1过点($\sqrt{3}$,$\frac{1}{2}$),离心率为$\frac{\sqrt{3}}{2}$,∴$\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}$=1,$\frac{c}{a}=\frac{\sqrt{3}}{2}$,又a2=b2+c2,
联立解得a=2,b=1,可得曲线C1的方程为:$\frac{{x}^{2}}{4}$+y2=1.(y≥0).
可得A(-2,0),∵点A在曲线C2上,∴0=4n-1,解得n=$\frac{1}{4}$,可得方程:y=$\frac{1}{4}$x2-1(y<0).
(II)解:A(-2,0),B(0,1),可得直线AB的方程:$\frac{x}{-2}+\frac{y}{1}$=1,化为:x-2y+2=0.
由题意可知:当曲线C2在点Q处的切线与直线AB平行时,△QAB的面积最大,
设切线方程为:x-2y+t=0,可知:切线斜率为$\frac{1}{2}$,y′=$\frac{1}{2}x$,
设切点Q(xQ,yQ),则$\frac{1}{2}{x}_{Q}$=$\frac{1}{2}$,解得xQ=1,∴yQ=$\frac{1}{4}-1$=-$\frac{3}{4}$,可得Q$(1,-\frac{3}{4})$.
代入切线方程可得t=-$\frac{5}{2}$,可得:切线方程为2x-4y-5=0.
此时△QAB的AB边上的高h=$\frac{|2-(-\frac{5}{2})|}{\sqrt{5}}$=$\frac{9\sqrt{5}}{10}$.
∴S△QAB的最大值=$\frac{1}{2}$|AB|h=$\frac{1}{2}×\sqrt{5}$×$\frac{9\sqrt{5}}{10}$=$\frac{9}{4}$,
∴△QAB面积的最大值为$\frac{9}{4}$,此时Q$(1,-\frac{3}{4})$.
(III)证明:由题意可得:k≠0,F$(\sqrt{3},0)$,N$(-\frac{m}{k},0)$.
设切点M(x0,y0),由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,化为:(1+4k2)x2+8kmx+4m2-4=0,
又直线l与曲线C1相切于点M,∴△=(8km)2-4(1+4k2)(4m2-4)=0,即m2=4k2+1.
x0=$\frac{1}{2}×$$(-\frac{8km}{1+4{k}^{2}})$=-$\frac{4km}{1+4{k}^{2}}$,y0=kx0+m=$\frac{m}{1+4{k}^{2}}$,∴M$(-\frac{4km}{1+4{k}^{2}},\frac{m}{1+4{k}^{2}})$,即M$(-\frac{4k}{m},\frac{1}{m})$.
可得N$(\frac{4\sqrt{3}}{3},\frac{4\sqrt{3}k}{3}+m)$,∴$\overrightarrow{FM}$=$(-\frac{4k}{m}-\sqrt{3},\frac{1}{m})$,$\overrightarrow{FN}$=$(\frac{\sqrt{3}}{3},\frac{4\sqrt{3}k}{3}+m)$,
∴$\overrightarrow{FM}•\overrightarrow{FN}$=$(-\frac{4k}{m}-\sqrt{3})×\frac{\sqrt{3}}{3}$+$\frac{1}{m}•$$(\frac{4\sqrt{3}k}{3}+m)$=0,
∴以MN为直径的圆过点F.
点评 本题考查了椭圆与圆的标准方程及其性质、直线与抛物线相切问题、直线相交问题、三角形面积计算公式、平行线之间的距离公式、导数的几何意义,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
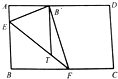 如图,有一张长为16,宽为8的矩形纸片ABCD,以EF为折痕(E在边AB上,F在边BC或CD上),使每次折叠后点B都落在AD边上,此时将B记为B′,过B′作B′T∥CD交EF于T点,则T点的轨迹所在的曲线是( )
如图,有一张长为16,宽为8的矩形纸片ABCD,以EF为折痕(E在边AB上,F在边BC或CD上),使每次折叠后点B都落在AD边上,此时将B记为B′,过B′作B′T∥CD交EF于T点,则T点的轨迹所在的曲线是( )| A. | 双曲线的一支 | B. | 椭圆 | C. | 抛物线 | D. | 直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(α)<g(λ)<g(β)<g(μ) | B. | g(λ)<g(α)<g(β)<g(μ) | C. | g(λ)<g(α)<g(μ)<g(β) | D. | g(α)<g(λ)<g(μ)<g(β) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com