
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若在区间![]() 上存在不相等的实数
上存在不相等的实数![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】
试题分析:(Ⅰ)将![]() 代入函数的表达式,求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;(Ⅱ)问题转化为求使函数
代入函数的表达式,求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;(Ⅱ)问题转化为求使函数![]() 在
在![]() 上不为单调函数的
上不为单调函数的![]() 的取值范围,通过讨论
的取值范围,通过讨论![]() 的范围,得到函数的单调性,进而求出
的范围,得到函数的单调性,进而求出![]() 的范围;(Ⅲ)先求出函数的导数,找到函数的极值点,从而证明出结论.
的范围;(Ⅲ)先求出函数的导数,找到函数的极值点,从而证明出结论.
试题解析:(Ⅰ)当![]() 时,
时,![]() ,
,![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 时,
时,![]() >0,f(x)单调递增;
>0,f(x)单调递增;
当![]() 时,
时,![]() <0,f(x)单调递减;
<0,f(x)单调递减;
当![]() 时,
时,![]() >0,f(x)单调递增.
>0,f(x)单调递增.
所以函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]()
(Ⅱ)依题意即求使函数![]() 在
在![]() 上不为单调函数的
上不为单调函数的![]() 的取值范围.
的取值范围.
![]() .设
.设![]() ,则
,则![]() ,
,![]() .
.
因为函数![]() 在
在![]() 上为增函数,当
上为增函数,当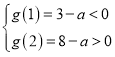 ,
,
即当![]() 时,函数
时,函数![]() 在
在![]() 上有且只有一个零点,设为
上有且只有一个零点,设为![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 为增函数,
为增函数,
满足在![]() 上不为单调函数.
上不为单调函数.
当![]() 时,
时,![]() ,
,![]() ,所以在
,所以在![]() 上
上![]() 成立
成立
(因![]() 在
在![]() 上为增函数),所以在
上为增函数),所以在![]() 上
上![]() 成立,
成立,
即![]() 在
在![]() 上为增函数,不合题意.
上为增函数,不合题意.
同理![]() 时,可判断
时,可判断![]() 在
在![]() 上为减函数,不合题意.综上
上为减函数,不合题意.综上![]()
(Ⅲ) ![]() .
.
因为函数![]() 有两个不同的极值点,即
有两个不同的极值点,即![]() 有两个不同的零点,
有两个不同的零点,
即方程![]() 的判别式
的判别式![]() ,解得
,解得![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
此时![]() ,
,![]() .
.
随着![]() 变化时,
变化时,![]() 和
和![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
| + |
| - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以![]() 是函数
是函数![]() 的极大值点,
的极大值点,![]() 是函数
是函数![]() 的极小值点.
的极小值点.
所以![]() 为极大值,
为极大值,![]() 为极小值.
为极小值.
![]() 所以
所以![]()
![]()
![]()
![]()
![]()
因为![]() ,所以
,所以![]() .所以
.所以![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率
的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程;
(2)设![]() 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过![]() 作直线交椭圆于
作直线交椭圆于![]() 两点,求△
两点,求△![]() 的内切圆半径
的内切圆半径![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是( )
A. 对立事件 B. 互斥但不对立事件
C. 不可能事件 D. 必然事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥P﹣ABCD如图.
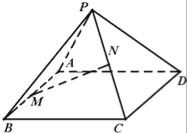
(Ⅰ)若其正视图是一个边长分别为![]() 、
、![]() ,2的等腰三角形,求其表面积S、体积V;
,2的等腰三角形,求其表面积S、体积V;
(Ⅱ)设AB中点为M,PC中点为N,证明:MN∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】6月23日15时前后,江苏盐城市阜宁、射阳等地突遭强冰雹、龙卷风双重灾害袭击,风力达12级.灾害发生后,有甲、乙、丙、丁4个轻型救援队从A,B,C,D四个不同的方向前往灾区.已知下面四种说法都是正确的.
(1)甲轻型救援队所在方向不是C方向,也不是D方向;
(2)乙轻型救援队所在方向不是A方向,也不是B方向;
(3)丙轻型救援队所在方向不是A方向,也不是B方向;
(4)丁轻型救援队所在方向不是A方向,也不是D方向;
此外还可确定:如果丙所在方向不是D方向,那么甲所在方向就不是A方向,有下列判断:
①甲所在方向是B方向;②乙所在方向是D方向;③丙所在方向是D方向;④丁所在方向是C方向.
其中判断正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:

(I)写出![]() 的值;
的值;
(II)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取3人,并用![]() 表示其中男生的人数,求
表示其中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80 C.120 D.180
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com