
(1)已知函数 ,过点P
,过点P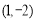 的直线
的直线 与曲线
与曲线 相切,求
相切,求 的方程;
的方程;
(2)设 ,当
,当 时,
时, 在1,4上的最小值为
在1,4上的最小值为 ,求
,求 在该区间上的最大值.
在该区间上的最大值.
(1) 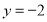 或
或 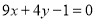 (2) 最大值为
(2) 最大值为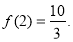
【解析】
试题分析:
(1) 根据题意可知,直线过点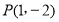 ,但是并没有说明该点是不是切点,所以得设出切点坐标,根据导数的几何意义可知,曲线切线的斜率就是在切点横坐标处的导数,然后利用点斜式求得切线方程;代入点
,但是并没有说明该点是不是切点,所以得设出切点坐标,根据导数的几何意义可知,曲线切线的斜率就是在切点横坐标处的导数,然后利用点斜式求得切线方程;代入点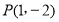 可求出切点,从而得切线方程.
可求出切点,从而得切线方程.
(2)首先利用导数求得极值点和函数的单调区间,根据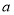 的范围可判断出函数在所给区间
的范围可判断出函数在所给区间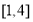 上的单调性,从而得出在该区间上的最小值(含
上的单调性,从而得出在该区间上的最小值(含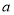 ),令其等于
),令其等于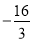 可得
可得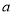 ,从而求出在该区间的最大值.
,从而求出在该区间的最大值.
试题解析:
(1)根据题意可知,直线过点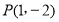 ,但是并没有说明该点是不是切点,所以设切点为
,但是并没有说明该点是不是切点,所以设切点为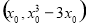 ,
,
因为函数的导函数为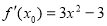 ,
,
所以根据导数的几何意义可知,切线的斜率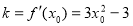 ,
,
则利用点斜式可得:切线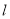 的方程
的方程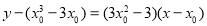 .
.
因为过点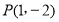 ,所以
,所以 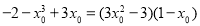 ,
,
解得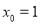 或
或 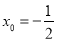
故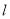 的方程为
的方程为 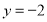 或
或 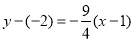 ,
,
即 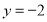 或
或 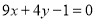 .
.
(2)令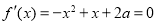 得
得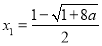 ,
,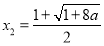 ,
,
故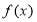 在
在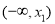 上递减,在
上递减,在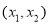 上递增,在
上递增,在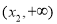 上递减.
上递减.
当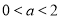 时,有
时,有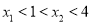 ,所以
,所以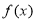 在
在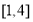 上的最大值为
上的最大值为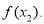
又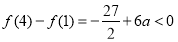 ,即
,即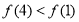 .
.
所以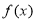 在
在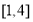 上的最小值为
上的最小值为 ,得
,得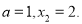
故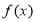 在
在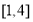 上的最大值为
上的最大值为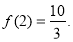
考点:导数法求切线方程;导数法求单调性和最值.


科目:高中数学 来源:2015届山东省高二下学期期中检测理科数学试卷(解析版) 题型:选择题
由直线x=- ,x=
,x= ,y=0与曲线y=cosx所围成的封闭图形的面积为( )
,y=0与曲线y=cosx所围成的封闭图形的面积为( )
A. B.1 C.
B.1 C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
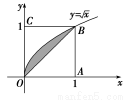
A. B.
B. C.
C.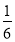 D.
D.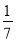
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com