Question

14．已知函数f（x）=e^x-1，g（x）=ln（x+1），直线l与y=f（x）的图象相切，与y=g（x）的图象也相切，则直线的l方程是y=x．

Answer 1

分析 由已知函数解析式画出图象，可得两函数有唯一交点O（0，0），求出两函数在O（0，0）处的切线都是y=x，则答案可求．

解答 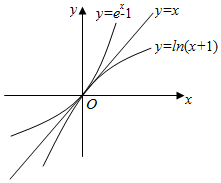解：f（x）=e^x-1与g（x）=ln（x+1）互为反函数，其图象如图，

其公共点为O（0，0），
由f（x）=e^x-1，得f′（x）=e^x，
∴f′（0）=1，
曲线f（x）=e^x-1在O（0，0）处的切线方程为y=x，
由g（x）=ln（x+1），得g′（x）=$\frac{1}{x+1}$，
∴g′（0）=1，
曲线g（x）=ln（x+1）在O（0，0）处的切线方程为y=x，
∴曲线f（x）=e^x-1与曲线g（x）=ln（x+1）的公切线为y=x．
故答案为：y=x．

点评 本题考查利用导数研究过曲线上某点处的切线方程，过曲线上某点处的切线的斜率，就是函数在该点处的导数值，是中档题．