Question

过点P(2，4)作两条互相垂直的直线l₁、l₂，若l₁交x轴于A点，l₂交y轴于B点，求线段AB的中点M的轨迹方程.?

Answer 1

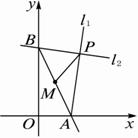
解法一:设点M的坐标为(x，y).?

∵M为线段AB的中点，

∴A的坐标为(2x，0)，B的坐标为(0，2y).?

∵l₁⊥l₂，且l₁、l₂过点P(2，4)，

∴PA⊥PB，k _PA·k_PB=-１.

而k _PA= (x≠1)，

?k _PB=，

∴·=-1(x≠1).?

整理，得x+2y-5=0(x≠1).?

∵当x=1时，A、B的坐标分别为(2，0)、(0，4),

∴线段AB的中点坐标是(1，2)，它满足方程 x+2y-5=0.?

综上所述，点M的轨迹方程是x+2y-5=0.

解法二:设M的坐标为(x，y)，则A、B两点的坐标分别是(2x，0)、(0，2y)，连结PM.

∵l₁⊥l₂，?∴2|PM|=|AB|.?

而|PM|=[KF(](x-2)²+(y-4)²[KF)]，

 

|AB|=，?

?∴2=.

化简，得x+2y-5=0为所求轨迹方程.

解法三:∵l₁⊥l₂，OA⊥OB，?

∴O、A、P、B四点共圆，且该圆的圆心为M.?

∴|MP|=|MO|.?

∴点M的轨迹为线段OP的中垂线.?

∵k _OP= =2，OP的中点坐标为(1，2)，

∴点M的轨迹方程是y-2=-(x-1)，

即x+2y-5=0.

温馨提示:在平面直角坐标系中，遇到垂直问题，常利用斜率之积等于-1解题，但需注意斜率是否存在，即往往需要讨论，如解法一.求轨迹方程有时利用平面几何知识更为方便快捷.