
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() 在区间
在区间![]() 内有两个极值点,求实数a的取值范围.
内有两个极值点,求实数a的取值范围.
【答案】(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增. (2)
上单调递增. (2)![]()
【解析】
(1)求出函数的导数,解关于导函数的方程,求出函数的单调区间,求出函数的极值即可;
(2)求出函数的导数,通过讨论![]() 的范围,求出函数的单调区间,结合函数的零点个数确定
的范围,求出函数的单调区间,结合函数的零点个数确定![]() 的范围即可.
的范围即可.
解:(1)由题意可得![]() 的定义域为
的定义域为![]() ,
,
![]()
当![]() 时,易知
时,易知![]()
∴由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)可得![]() ,
,
当![]() 时,
时,![]() ,
,
记![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 内有两个极值点,
内有两个极值点,
∴![]() 在
在![]() 内有两个零点,
内有两个零点,
∴![]() .
.
令![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,所以在
,所以在![]() 上单调递减,
上单调递减,
![]() 的图像至多与x轴有一个交点,不满足题意.
的图像至多与x轴有一个交点,不满足题意.
当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递增,
单调递增,
![]() 的图像至多与x轴有一个交点,不满足题意.
的图像至多与x轴有一个交点,不满足题意.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
由![]() 知,要使
知,要使![]() 在
在![]() 内有两个零点,必须满足
内有两个零点,必须满足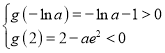 ,解得
,解得![]() .
.
综上,实数a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位
平均增加5个单位
③线性回归方程![]() 必过
必过![]()
④设具有相关关系的两个变量![]() 的相关系数为
的相关系数为![]() ,那么
,那么![]() 越接近于0,
越接近于0,![]() 之间的线性相关程度越高;
之间的线性相关程度越高;
⑤在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,那么
的值,那么![]() 的值越大,判断两个变量间有关联的把握就越大。
的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“不忘初心、牢记使命”主题教育活动正在全国开展,某区政府为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n名,获得了他们一周参加主题教育活动的时间(单位:时)的频率分布直方图,如图所示,已知参加主题教育活动的时间在![]() 内的人数为92.
内的人数为92.
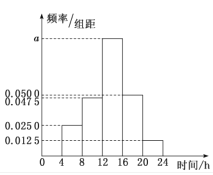
(1)估计这些党员干部一周参与主题教育活动的时间的平均值;
(2)用频率估计概率,如果计划对全区一周参与主题教育活动的时间在![]() 内的党员干部给予奖励,且参与时间在
内的党员干部给予奖励,且参与时间在![]() ,
,![]() 内的分别获二等奖和一等奖,通过分层抽样方法从这些获奖人中随机抽取5人,再从这5人中任意选取3人,求3人均获二等奖的概率.
内的分别获二等奖和一等奖,通过分层抽样方法从这些获奖人中随机抽取5人,再从这5人中任意选取3人,求3人均获二等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为
的左、右焦点为别为![]() 、
、![]() ,且过点
,且过点![]() 和
和![]() .
.
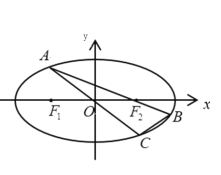
(1)求椭圆的标准方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,
,![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某北方村庄4个草莓基地,采用水培阳光栽培方式种植的草莓个大味美,一上市便成为消费者争相购买的对象.光照是影响草莓生长的关键因素,过去50年的资料显示,该村庄一年当中12个月份的月光照量X(小时)的频率分布直方图如下图所示(注:月光照量指的是当月阳光照射总时长).
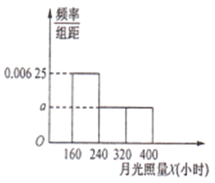
(1)求月光照量![]() (小时)的平均数和中位数;
(小时)的平均数和中位数;
(2)现准备按照月光照量来分层抽样,抽取一年中的4个月份来比较草莓的生长状况,问:应在月光照量![]() ,
,![]() ,
,![]() 的区间内各抽取多少个月份?
的区间内各抽取多少个月份?
(3)假设每年中最热的5,6,7,8,9,10月的月光照量![]() 是大于等于240小时,且6,7,8月的月光照量
是大于等于240小时,且6,7,8月的月光照量![]() 是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量
是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量![]() (小时)都不低于320的概率.
(小时)都不低于320的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=![]() a(0<
a(0<![]() ≦1). w.w.w..c.o.m
≦1). w.w.w..c.o.m
(Ⅰ)求证:对任意的![]()
![]() (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.

(Ⅰ)证明:AB1⊥平面A1B1C1;
(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com