
分析 (1)根据不等式f(x)>-2x的解集为(1,3)得出x=1和x=3是方程ax2+(b+2)x+c=0(a<0)的两根列出关于a,b的等式再根据方程f(x)+6a=0有两个相等的实根得到:△=0求得a值,从而得到f(x)的解析式;
(2)问题转化为只需[-1,0]?[-3,m]成立即可.
解答 解:(1)∵方程f(x)+2x=0有两个实根x1=1,x2=3,
∴x=1和x=3是方程ax2+(b+2)x+c=0(a>0)的两根
∴$\left\{\begin{array}{l}{\frac{b+2}{a}=-4}\\{\frac{c}{a}=3}\end{array}\right.$,∴b=-4a-2,c=3a
又方程f(x)+6a=0有两个相等的实根
∴△=b2-4a(c+6a)=0
∴4(2a+1)2-4a×9a=0
∴(5a+1)(1-a)=0
∴a=-$\frac{1}{5}$(舍)或a=1,
∴a=1,b=-6,c=3,
∴f(x)=x2-6x+3;
(2)∵f(x)的图象与x轴交于A(-3,0)B(m,0)两点,
当-1≤x≤0时,f(x)≤0恒成立,
只需[-1,0]?[-3,m],
∴m≥0.
点评 本小题主要考查函数的最值及其几何意义、函数与方程的综合运用,考查运算求解能力,与转化思想.属于基础题


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
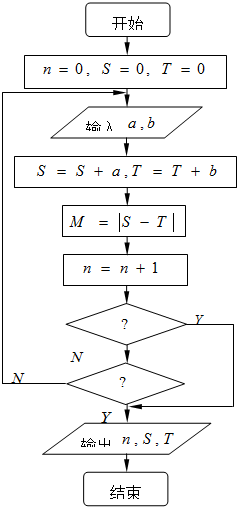 在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )
在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )| A. | M≥2,n>5 | B. | M=2,n=6 | C. | M>1,n≥6 | D. | M≥2,n<7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{3}{2}$] | B. | [-1,4] | C. | [-5,5] | D. | [-3,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com