
分析 (1)根据题意,将原问题转化为20个小球的分组问题:假设有20个完全相同的小球,将其排成一列,利用挡板法将其分成4组,四个小组的小球数目分别对应x1、x2、x3、x4,由组合数公式计算即可得答案;
(2)由(1)假设有104个完全相同的小球,将其排成一列,共有103个空位,可得方程的非负整数解的组数;
(3)分类讨论,即可得出结论.
解答 解:(1)假设有100个完全相同的小球,将其排成一列,共有99个空位,
在其中选3个,插入挡板,即可将100个小球分成4组,有C993种分组方法;
第一组小球的数目是x1,第二组小球的数目是x2,第三组小球的数目是x3,第四组小球的数目是x4,
则方程的正整数解的组数就是C993;
(2)由(1)假设有104个完全相同的小球,将其排成一列,共有103个空位,方程的非负整数解的组数是C1033;
(3)x1+x2=3 (1组) x3+x4=97 (91组)
x1+x2=4 (2组) x3+x4=96 (90组)
x1+x2=5 (3组) x3+x4=95 (89组)
…
x1+x2=93 (91组) x3+x4=7 (1组)
总组数=1×91+2×90+3×89+…+91×1=129766.
点评 本题考查排列、组合的应用,关键在于将原问题进行转化,进而运用挡板法求解.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
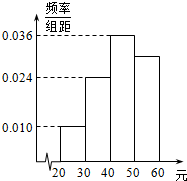 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.| A. | 45 | B. | 46 | C. | $\frac{390}{9}$ | D. | $\frac{400}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [75,90] | 5 | 0.05 |
| 第2组 | (90,105] | ① | 0.35 |
| 第3组 | (105,120] | 30 | ② |
| 第4组 | (120,135] | 20 | 0.20 |
| 第5组 | (135,150] | 10 | 0.10 |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com