
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [75,90] | 5 | 0.05 |
| 第2组 | (90,105] | ① | 0.35 |
| 第3组 | (105,120] | 30 | ② |
| 第4组 | (120,135] | 20 | 0.20 |
| 第5组 | (135,150] | 10 | 0.10 |
| 合计 | 100 | 1.00 | |
分析 (Ⅰ)由题意利用频率=$\frac{频数}{总数}$,能求出频率分布表中①、②位置相应的数据.
(Ⅱ)因为第3、4、5组共有60名学生,由此能求出利用分层抽样在60名学生中抽取6名学生,第3、4、5组分别抽取的人数.
(Ⅲ)利用列举法求出从六位同学中抽两位同学的基本事件总数和第4组的2位同学为b至少有一位同学入选包含的基本事件个数,由此能求出第4组至少有一名学生被抽查的概率.
解答 解:(Ⅰ)由题可知,第2组的频数为0.35×100=35人 …(1分)
第3组的频率为$\frac{30}{100}=0.30$…(2分)
(Ⅱ)因为第3、4、5组共有60名学生,
所以利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组:$\frac{30}{60}×6=3$人…(3分)
第4组:$\frac{20}{60}×6=2$人…(4分)
第5组:$\frac{10}{60}×6=1$人
所以第3、4、5组分别抽取3人、2人、1人 …(5分)
(Ⅲ)设第3组的3位同学为A1,A2,A3第4组的2位同学为B1,B2,第5组的l位同学为C1
则从六位同学中抽两位同学有15种可能如下:(A1,A2),(A1,A3),(A1,B1),
(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),
(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),…(8分)
其中第4组的2位同学为b至少有一位同学入选的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),
(A3,B2),(B1,B2),(B1,C1),(B2,C1)9种可能 …(10分)
所以第4组至少有一名学生被抽查的概率为p=$\frac{9}{15}=\frac{3}{5}$.…(12分)
点评 本题考查频率分布表的应用,考查分层抽样的性质,考查概率的求法,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
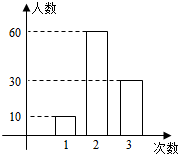 某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动),该校合唱团共有100名学生,他们参加活动的次数统计如图所示;
某中学号召学生在今年暑假期间至少参加一次社会公益活动(以下简称活动),该校合唱团共有100名学生,他们参加活动的次数统计如图所示;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
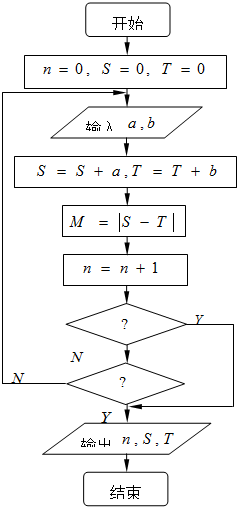 在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )
在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )| A. | M≥2,n>5 | B. | M=2,n=6 | C. | M>1,n≥6 | D. | M≥2,n<7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com