练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．阅读如图所示的程序语句，若运行程序，则输出结果为（　　）
    A．1B．2C．0D．-1

    分析 由已知中的程序语句可知：该程序的功能是利用条件结构计算并输出变量a+b+c，或a-b-c的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

    解答 解：执行完a=1后，a=1，
    执行完b=a-2后，a=1，b=-1；
    执行完c=a-b后，a=1，b=-1，c=2；
    此时不满足条件c＜a，
    故输出a-b-c=0，
    故选：C

    点评 本题考查了程序框图的应用问题，分析出程序的功能是解答的关键，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知m＞0，两圆x2+y2=m与x2+（y-m）2=20相交于A，B两点，且在点A处两圆的切线互相垂直，则线段AB的长度为（　　）
    A．3B．3$\sqrt{2}$C．4D．4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设a，b，c∈R+，求证：a+b+c≤$\frac{{a}^{2}+{b}^{2}}{2c}$+$\frac{{b}^{2}+{c}^{2}}{2a}$+$\frac{{c}^{2}+{a}^{2}}{2b}$≤$\frac{{a}^{3}}{bc}$+$\frac{{b}^{3}}{ca}$+$\frac{{c}^{3}}{ab}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

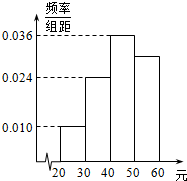    12．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n且支出在[20，60）元的样本，其频率分布直方图如图所示，根据此图估计学生在课外读物方面的支出费用的中位数为（　　）元．
    A．45B．46C．$\frac{390}{9}$D．$\frac{400}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．中国女子乒乓球队参加某团体项目决赛，已知团体赛采用“五局三胜”制，第一、二、四、五局为单打，第三局为双打，且一个队由三名运动员组成，每名运动员出场两次，根据历次大型比赛的统计，中国女子乒乓球队单打获胜的概率为$\frac{3}{5}$，双打获胜的概率为$\frac{3}{4}$，若在决赛的第一局中，由于中国队选手准备不够充分，输掉了这一局．
    （1）求中国女子乒乓球队夺得团体冠军的概率；
    （2）设决赛中比赛总的局数为ξ，求ξ的分布列及数学期望．（两问均用分数作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．某程序框图如图所示，当输出y值为-8时，则输出x的值为（　　）
    A．64B．32C．16D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某驾校为了保证学员科目二考试的通过率，要求学员在参加正式考试（下面简称正考）之前必须参加预备考试（下面简称预考），且在预考过程中评分标准得以细化，预考成绩合格者才能参加正考．现将10名学员的预考成绩绘制成茎叶图如图所示：
    规定预考成绩85分以上为合格，不低于90分为优秀．若上述数据的中位数为85.5，平均数为83．
    （1）求m，n的值，指出该组数据的众数，并根据平均数以及参加正考的成绩标准对该驾校学员的学习情况作简单评价；
    （2）若在上述可以参加正考的学员中随机抽取2人，求其中恰有1人成绩优秀的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某高中在一次数学考试中随机抽取100名学生的成绩，按成绩分组，得到的频率分布表如图所示
    组号分组频数频率
    第1组[75，90]50.05
    第2组（90，105]①0.35
    第3组（105，120]30②
    第4组（120，135]200.20
    第5组（135，150]100.10
    合计1001.00
    （Ⅰ）求出频率分布表中①、②位置相应的数据；
    （Ⅱ）为了能选拔出最优秀的学生参加数学竞赛，学校决定在成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮测试，求第3、4、5组每组各抽取多少名学生进入第二轮测试？
    （Ⅲ）在（Ⅱ）的前提下，学校决定在6名学生中随机抽取2名学生进行抽查，求第4组至少有一名学生被抽查的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若tan（θ+$\frac{π}{4}$）=-3，则$\frac{sin2θ}{1+cos2θ}$=（　　）
    A．-1B．1C．-2D．2

    查看答案和解析>>

    同步练习册答案