
分析 (1)对分式分解,利用均值定理可得.
(2)构造函数f(x)=$\frac{x}{1+x}$=1-$\frac{1}{1+x}$;只需判断函数的单调性即可.
解答 解:(1)∵$\frac{b+c-a}{a}$+$\frac{a+c-b}{b}$+$\frac{a+b-c}{c}$
=$\frac{b}{a}$+$\frac{c}{a}$+$\frac{a}{b}$+$\frac{c}{b}$+$\frac{a}{c}$+$\frac{b}{c}$-3
∵a,b,c是全不相等的正实数,
∴$\frac{b}{a}$+$\frac{c}{a}$+$\frac{a}{b}$+$\frac{c}{b}$+$\frac{a}{c}$+$\frac{b}{c}$-3
=$\frac{b}{a}$+$\frac{a}{b}$+$\frac{c}{a}$+$\frac{a}{c}$+$\frac{c}{b}$+$\frac{b}{c}$-3>6-3=3;
(2)令f(x)=$\frac{x}{1+x}$=1-$\frac{1}{1+x}$;
由1+x递增,得f(x)在(0,+∞)为增函数,
∵a+b>c,
∴f(a+b)>f(c)
∴$\frac{a+b}{1+a+b}>\frac{c}{1+c}$.
点评 考查了均值定理和利用函数证明不等式.难点是函数的构造,应细心观察.


科目:高中数学 来源: 题型:选择题
| A. | t≤-3 | B. | t<-3 | C. | t≥-3 | D. | t>-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
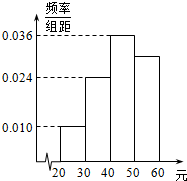 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.| A. | 45 | B. | 46 | C. | $\frac{390}{9}$ | D. | $\frac{400}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [75,90] | 5 | 0.05 |
| 第2组 | (90,105] | ① | 0.35 |
| 第3组 | (105,120] | 30 | ② |
| 第4组 | (120,135] | 20 | 0.20 |
| 第5组 | (135,150] | 10 | 0.10 |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com