
分析 首先确定函数的定义域,并判断其定义域是否关于原点对称,然后确定f(-x)与f(x)的关系,注意到$\sqrt{1{+x}^{2}}$-x与$\sqrt{1{+x}^{2}}$+x互为倒数关系.
解答 解:函数的定义域为R,
f(-x)=lg($\sqrt{1{+x}^{2}}$-x)=lg($\sqrt{1{+x}^{2}}$+x)-1=-lg($\sqrt{1{+x}^{2}}$+x)=-f(x),
故该函数是奇函数.
点评 本题考查了函数的奇偶性的判定,以及对数的运算性质,属于基础题.定义域关于原点对称是奇偶函数的一个本质特征,定义法是其它方法的基础;用等价定义判断解析式较为复杂的函数的奇偶性时,可化繁为简;图象关于原点或y轴对称是奇偶函数的几何特征;反之,函数的奇偶性又是函数图象对称性的代数描述,进而实现了数与形的辨证统一.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{27}$ | B. | $\frac{1}{27}$ | C. | $\frac{2}{9}$ | D. | $\frac{26}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
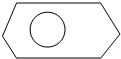 如图,在一个不规则多边形内随机撒入200粒麦粒(麦粒落到任何位置可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒麦粒(麦粒落到任何位置可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com