
【题目】无穷数列![]()
![]() ,若存在正整数
,若存在正整数![]() ,使得该数列由
,使得该数列由![]() 个互不相同的实数组成,且对于任意的正整数
个互不相同的实数组成,且对于任意的正整数![]() ,
,![]() 中至少有一个等于
中至少有一个等于![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .集合
.集合![]() .
.
(1)若![]() ,
,![]() ,判断数列
,判断数列![]() 是否具有性质
是否具有性质![]() ;
;
(2)数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)数列![]() 具有性质
具有性质![]() ,对于
,对于![]() 中的任意元素
中的任意元素![]() ,
,![]() 为第
为第![]() 个满足
个满足![]() 的项,记
的项,记![]()
![]() ,证明:“数列
,证明:“数列![]() 具有性质
具有性质![]() ”的充要条件为“数列
”的充要条件为“数列![]() 是周期为
是周期为![]() 的周期数列,且每个周期均包含
的周期数列,且每个周期均包含![]() 个不同实数”.
个不同实数”.
【答案】(1)具有;(2)2;(3)答案见解析.
【解析】试题分析:
(1)由题意可知![]() 是周期为2的周期数列,对于任意的正整数
是周期为2的周期数列,对于任意的正整数![]() ,
,![]() ,满足性质
,满足性质![]() 的条件,故数列
的条件,故数列![]() 具有性质
具有性质![]() .
.
(2)由条件可知![]() ,考虑
,考虑![]() 后面连续三项
后面连续三项![]() ,由反证法可知
,由反证法可知![]() .同理可得
.同理可得![]() .
.
(3)充分性:由数列![]() 是周期为
是周期为![]() 的周期数列,每个周期均包含
的周期数列,每个周期均包含![]() 中
中![]() 个不同元素.则由周期性得
个不同元素.则由周期性得![]() ,于是数列
,于是数列![]() 为常数列,显然满足性质
为常数列,显然满足性质![]() .
.
必要性:取足够大的![]() 使
使![]() 包含
包含![]() 中所有
中所有![]() 个互不相同的元素,考虑
个互不相同的元素,考虑![]() 后的连续
后的连续![]() 项
项![]() ,由反证法可知
,由反证法可知![]() 中任意元素
中任意元素![]() ,必等于
,必等于![]() 中的某一个,再由数列
中的某一个,再由数列![]() 性质
性质![]() 中的条件得
中的条件得![]() ,
,![]() ,则数列
,则数列![]() 为常数列,
为常数列,![]() 为常数列,据此可得数列
为常数列,据此可得数列![]() 是周期为
是周期为![]() 的周期数列,且每个周期均包含
的周期数列,且每个周期均包含![]() 个不同实数.
个不同实数.
试题解析:
(1)因为![]() ,
,![]() ,
,![]() 是由2个不同元素组成的无穷数列,且是周期为2的周期数列,故
是由2个不同元素组成的无穷数列,且是周期为2的周期数列,故![]() ,
,![]() 是周期为2的周期数列,对于任意的正整数
是周期为2的周期数列,对于任意的正整数![]() ,
,![]() ,满足性质
,满足性质![]() 的条件,故数列
的条件,故数列![]() 具有性质
具有性质![]() .
.
(2)![]() .由条件可知
.由条件可知![]() ,考虑
,考虑![]() 后面连续三项
后面连续三项![]() ,若
,若![]() ,
,
由![]() 及
及![]() 性质知
性质知![]() 中必有一数等于2,
中必有一数等于2,
于是![]() 中有两项为2,故必有1或3不在其中,
中有两项为2,故必有1或3不在其中,
不妨设为![]() ,考虑
,考虑![]() 中最后一个等于
中最后一个等于![]() 的项,
的项,
则该项的后三项均不等于![]() ,故不满足性质
,故不满足性质![]() 中条件,矛盾,
中条件,矛盾,
于是![]() .同理
.同理![]() .
.
(3)充分性:由数列![]() 是周期为
是周期为![]() 的周期数列,每个周期均包含
的周期数列,每个周期均包含![]() 中
中![]() 个不同元素.
个不同元素.
对于![]() 中的任意元素
中的任意元素![]() ,
,![]() 为第
为第![]() 个满足
个满足![]() 的项,
的项,
故由周期性得![]() ,
,
于是![]() ,数列
,数列![]() 为常数列,显然满足性质
为常数列,显然满足性质![]() .
.
必要性:取足够大的![]() 使
使![]() 包含
包含![]() 中所有
中所有![]() 个互不相同的元素,
个互不相同的元素,
考虑![]() 后的连续
后的连续![]() 项
项![]() ,
,
对于![]() 中任意元素
中任意元素![]() ,必等于
,必等于![]() 中的某一个,
中的某一个,
否则考虑![]() 中最后一个等于
中最后一个等于![]() 的项,该项不满足性质
的项,该项不满足性质![]() 中条件,矛盾.
中条件,矛盾.
由![]() 的任意性知
的任意性知![]() 这
这![]() 个元素恰好等于
个元素恰好等于![]() 中
中![]() 个互不相同的元素,
个互不相同的元素,
再由数列![]() 性质
性质![]() 中的条件得
中的条件得![]() ,
,![]() ,
,
于是对于![]() 中的任意元素
中的任意元素![]() ,存在
,存在![]() ,有
,有![]()
![]() ,
,
即数列![]() 为常数列,
为常数列,
而数列![]() 满足性质
满足性质![]() ,故
,故![]() 为常数列,
为常数列,
从而![]() 是周期数列,故数列
是周期数列,故数列![]() 是周期为
是周期为![]() 的周期数列,
的周期数列,
且每个周期均包含![]() 个不同实数.
个不同实数.


科目:高中数学 来源: 题型:
【题目】在研究塞卡病毒(Zika virus)某种疫苗的过程中,为了研究小白鼠连续接种该种疫苗后出现![]() 症状的情况,做接种试验,试验设计每天接种一次,连续接种3天为一个接种周期.已知小白鼠接种后当天出现
症状的情况,做接种试验,试验设计每天接种一次,连续接种3天为一个接种周期.已知小白鼠接种后当天出现![]() 症状的概率为
症状的概率为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若出现![]() 症状即停止试验,求试验至多持续一个接种周期的概率;
症状即停止试验,求试验至多持续一个接种周期的概率;
(2)若在一个接种周期内出现2次货3次![]() 症状,则这个接种周期结束后终止试验,试验至多持续3个周期,设接种试验持续的接种周期数为
症状,则这个接种周期结束后终止试验,试验至多持续3个周期,设接种试验持续的接种周期数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买![]() 黄金,售货员先将
黄金,售货员先将![]() 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将![]() 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金( )
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金( )
A. 大于![]() B. 小于
B. 小于![]() C. 大于等于
C. 大于等于![]() D. 小于等于
D. 小于等于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20世纪30年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用测震仪地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M,其计算公式为![]() 其中,A是被测量地震的最大振幅,
其中,A是被测量地震的最大振幅,![]() 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际的距离造成的偏差),众所周知,5级地震已经比较明显,计算8级地震的最大振幅是5级地震的最大振幅的______倍.
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际的距离造成的偏差),众所周知,5级地震已经比较明显,计算8级地震的最大振幅是5级地震的最大振幅的______倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对食堂伙食的满意程度,组织学生给食堂打分(分数为整数,满分100分),从中随机抽取一个容量为![]() 的样本,发现所有数据均在
的样本,发现所有数据均在![]() 内.现将这些分数分成以下
内.现将这些分数分成以下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
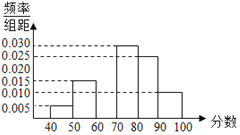
(1)算出第三组![]() 的频数,并补全频率分布直方图;
的频数,并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数和平均数,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01);(若
并加以说明(精确到0.01);(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如表关系:
限制,并有如表关系:

若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以过去50周的周光照量的频率作为周光照量发生的概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式 ,参考数据
,参考数据![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]()
![]() ,使得
,使得![]() 函数满足:(1)
函数满足:(1)![]() 在
在![]() 上是单调函数;(2)
上是单调函数;(2)![]() 在
在![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“和谐区间”,下列结论错误的是( )
的“和谐区间”,下列结论错误的是( )
A.函数![]() 存在“和谐区间”
存在“和谐区间”
B.函数![]() 不存在“和谐区间”
不存在“和谐区间”
C.函数![]()
![]() 存在“和谐区间”
存在“和谐区间”
D.函数![]() (
(![]() ,
,![]() )不存在“和谐区间”
)不存在“和谐区间”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com