练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知动圆过定点，且与定直线相切.

    （1）求动圆圆心的轨迹的方程；

    （2）若是轨迹的动弦，且过， 分别以、为切点作轨迹的切线，设两切线交点为，证明:.

    【答案】（1）（2）详见解析

    【解析】

    试题（I）由题意可得：动圆圆心到定点（0，2）与到定直线y=-2的距离相等，利用抛物线的定义求轨迹方程即可；（II）设AB：y=kx+2，将直线的方程代入抛物线的方程，消去y得到关于x的一元二次方程，再结合根与系数的关系利用切线的几何意义即可求得过抛物线上A、B两点的切线斜率关系，从而解决问题

    试题解析：（1）依题意，圆心的轨迹是以为焦点，为准线的抛物线

    因为抛物线焦点到准线距离等于4, 所以圆心的轨迹方程是

    （2）

    ，

    ，

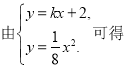
    抛物线方程为 所以过抛物线上A、B两点的切线斜率分别是

    ，.

    所以，

    (注:也可设,再由,设

    则直线AQ:,联立直线和抛物线方程,由直线和抛物线相切得

    可得，同理可得，从而证）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知O为坐标原点，椭圆C：的左、右焦点分别为，，右顶点为A，上顶点为B，若，，成等比数列，椭圆C上的点到焦点的距离的最大值为．

    求椭圆C的标准方程；

    过该椭圆的右焦点作倾角为的直线与椭圆交于M，N两点，求的内切圆的半径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关，随机抽取了选修课程的55名学生，得到数据如下表：

    喜欢统计课程

    不喜欢统计课程

    男生

    20

    5

    女生

    10

    20

    临界值参考：

    0.10

    0.05

    0.25

    0.010

    0.005

    0.001

    k

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式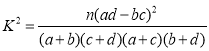：，其中）

    参照附表，得到的正确结论是（ ）

    A.在犯错误的概率不超过的前提下，认为“喜欢“应用统计”课程与性别有关”

    B.在犯错误的概率不超过的前提下，认为“喜欢“应用统计”课程与性别无关”

    C.有以上的把握认为“喜欢应用统计”课程与性别有关”

    D.有以上的把握认为“喜欢“应用统计”课程与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年春节期间，某超市准备举办一次有奖促销活动，若顾客一次消费达到400元则可参加一次抽奖活动，超市设计了两种抽奖方案.

    方案一：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得60元的返金券，若抽到白球则获得20元的返金券，且顾客有放回地抽取3次.

    方案二：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得80元的返金券，若抽到白球则未中奖，且顾客有放回地抽取3次.

    （1）现有两位顾客均获得抽奖机会，且都按方案一抽奖，试求这两位顾客均获得180元返金券的概率；

    （2）若某顾客获得抽奖机会.

    ①试分别计算他选择两种抽奖方案最终获得返金券的数学期望；

    ②为了吸引顾客消费，让顾客获得更多金额的返金券，该超市应选择哪一种抽奖方案进行促销活动？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，过点的直线的参数方程为（为参数），以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线的极坐标方程为.

    （1）若点的直角坐标为，求直线及曲线的直角坐标方程；

    （2）若点在上，直线与交于两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国清朝数学家李善兰在1859年翻译《代数学》中首次将“”译做：“函数”，沿用至今，为什么这么翻译，书中解释说“凡此变数中函彼变数者，则此为彼之函数”1930年美国人给出了我们课本中所学的集合论的函数定义，已知集合，，给出下列四个对应法则，请由函数定义判断，其中能构成从到的函数的是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知过原点O的直线与函数的图象交于A，B两点，分别过A，B作y轴的平行线与函数图象交于C，D两点，若轴，则四边形ABCD的面积为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在空间直角坐标系中，已知正四棱锥的高，点和分别在轴和轴上，且，点是棱的中点.

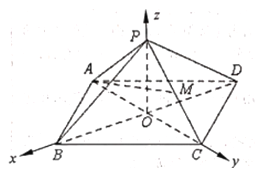
    （1）求直线与平面所成角的正弦值；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中正确的是（ ）

    A.对具有线性相关关系的变量有一组观测数据，其线性回归方程是，且，则实数的值是

    B.正态分布在区间和上取值的概率相等

    C.若两个随机变量的线性相关性越强，则相关系数的值越接近于1

    D.若一组数据的平均数是2，则这组数据的众数和中位数都是2

    查看答案和解析>>

    同步练习册答案