
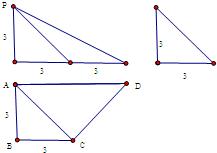
 已知四棱锥P-ABCD的三视图如图所示,
已知四棱锥P-ABCD的三视图如图所示,分析 (1)画出几何体的直观图,利用三视图得到数据,直接求解几何体是体积即可.
(2)分别求出两条直线所在的向量,利用向量的有关运算求出两个向量的夹角,进而转化为两条直线的夹角.
解答  解:(1)由题意可知几何体的直观图如图:
解:(1)由题意可知几何体的直观图如图:
可设PA⊥PD,PA⊥AB,AD⊥AB,DC⊥AD,则PA=3,AD=3,DC=3,AB=6,
几何体的体积为:V=$\frac{1}{3}{S}_{ABCD}•PA$=$\frac{1}{3}×\frac{3+6}{2}×3×3$=$\frac{27}{2}$.
(2)以A为坐标原点AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,
则各点坐标为A(0,0,0),B(0,6,0),C(3,3,0),D(3,0,0),P(0,0,3),
因$\overrightarrow{AC}$=(3,3,0),$\overrightarrow{PB}$=(0,6,-3),
故|$\overrightarrow{AC}$|=$3\sqrt{2}$,|$\overrightarrow{PB}$|=$3\sqrt{5}$,$\overrightarrow{AC}$•$\overrightarrow{PB}$=18,
所以cos<$\overrightarrow{AC}$,$\overrightarrow{PB}$>═$\frac{\overrightarrow{AC}•\overrightarrow{PB}}{\left|\overrightarrow{AC}\right|\left|\overrightarrow{PB}\right|}$=$\frac{18}{3\sqrt{2}×3\sqrt{5}}$=$\frac{\sqrt{10}}{5}$.
直线PB与直线AC所成角的大小是<$\overrightarrow{AC}$,$\overrightarrow{PB}$>=arccos$\frac{\sqrt{10}}{5}$.
故答案为:$\frac{27}{2}$;$arccos\frac{\sqrt{10}}{5}$.
点评 解决此类问题的关键是熟悉几何体的结构特征,有利于建立空间直角坐标系,利用向量的有关运算解决空间角与空间距离等问题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
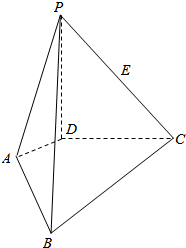 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
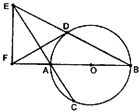 如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
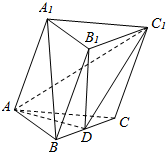 如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.
如图,三棱柱ABC-A1B1C1所有的棱长为2,B1在底面上的射影D在棱BC上,且A1B∥平面ADC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com