
分析 根据条件及平均值不等式,(3a+1)+(3b+1)+(3c+1)=3(a+b+c)+3≥12,而根据柯西不等式[(3a+1)+(3b+1)+(3c+1)]$(\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1})$≥9,这样便可得出$12(\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1})≥9$,从而得出$\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1}≥\frac{3}{4}$,当a=b=c=1时取“=”.
解答 证明:a,b,c为正数,abc=1;
∴(3a+1)+(3b+1)+(3c+1)=3(a+b+c)+3≥9$\root{3}{abc}+3$=12,当且仅当a=b=c时取“=”;
根据柯西不等式:[(3a+1)+(3b+1)+(3c+1)]($\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1}$)$≥(\sqrt{3a+1}•\frac{1}{\sqrt{3a+1}}+\sqrt{3b+1}•\frac{1}{\sqrt{3b+1}}+\sqrt{3c+1}•\frac{1}{\sqrt{3c+1}})^{2}=9$,当且仅当3a+1=3b+1=3c+1,即a=b=c=1时取“=”;
∴$12(\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1})≥9$,当a=b=c=1时取“=”;
∴$\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1}≥\frac{9}{12}=\frac{3}{4}$;
即$\frac{1}{3a+1}+\frac{1}{3b+1}+\frac{1}{3c+1}≥\frac{3}{4}$.
点评 考查平均值不等式及柯西不等式的形式,而根据柯西不等式的形式结合已知条件进行配凑,是解决本题的关键所在,注意等号成立的条件,判断等号能否同时成立.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
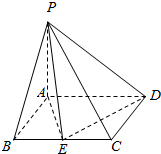 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
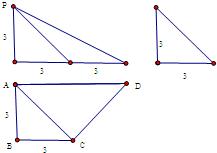 已知四棱锥P-ABCD的三视图如图所示,
已知四棱锥P-ABCD的三视图如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80种 | B. | 120种 | C. | 480种 | D. | 600种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
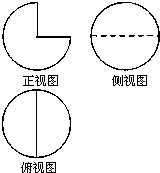
| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com