已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-1.
(1)求f(x)的解析式
(2)写出f(x)的单调区间;
(3)求满足f(-m)=f(m)的实数m的值.
解:(1)因为函数f(x)是定义在R上的奇函数,根据其对称性可知f(0)=0,
当x<0时,-x>0
则f(-x)=2(-x)-1=-f(x)
∴x<0时,f(x)=2x+1
∴f(x)=
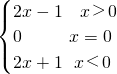
(2)当x>0时,f(x)=2x-1,根据一次函数的性质可知函数在(0,+∞)上单调递增
当x<0时,f(x)=2x+1,根据一次函数的性质可知函数在(-∞,0)上单调递增
∴f(x)在(-∞,0)、(0,+∞)上单调递增
(3)∵f(-m)=f(m),f(x)是定义在R上的奇函数
∴-f(m)=f(m)即f(m)=0
当m>0时,f(m)=2m-1=0,解得m=

当m=0时,f(0)=0,满足条件
当m<0时,f(m)=2m+1=0,解得m=-

∴满足f(-m)=f(m)的实数m的值为-

,0,

.
分析:(1)先根据奇函数的性质推断出f(0)=0,进而把-x代入x>0时函数的解析式,利用奇数函数的性质求得x<0的解析式,最后利用分段函数表示即可;
(2)根据一次函数的单调性与一次项系数的符号有关可分别判定函数在(-∞,0)与(0,+∞)上的单调性;
(3)先根据奇偶性可得f(m)=0,然后讨论m,根据函数值求相应的m即可.
点评:本题主要考查了函数的解析式,以及函数的奇偶性和求函数值,同时考查了分类讨论的数学思想,属于基础题.

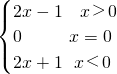


 ,0,
,0, .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案