
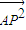 +
+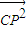 =
=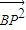 +
+ ,那么四边形ABCD一定是( )
,那么四边形ABCD一定是( ) +
+ =
= +
+ 建立等式关系,即可判定四边形的形状.
建立等式关系,即可判定四边形的形状. =(x,y),
=(x,y), ,
, =(x-xC,y-yc),
=(x-xC,y-yc),
 +
+ =
= +
+ ,
,
 ,则平行四边形ABCD为矩形
,则平行四边形ABCD为矩形

科目:高中数学 来源: 题型:
| 1 |
| 4 |
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源:天利38套《2009高考模拟试题汇编附加试题》、数学理科 题型:013
已知平面内的四边形ABCD和该平面内任一点P满足:![]() ,那么四边形ABCD一定是
,那么四边形ABCD一定是
A.梯形
B.菱形
C.矩形
D.正方形
查看答案和解析>>
科目:高中数学 来源:武汉模拟 题型:单选题
| AP2 |
| CP2 |
| BP2 |
| DP2 |
| A.梯形 | B.菱形 | C.矩形 | D.正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com