
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.

(1)设点P分有向线段![]() 所成的比为λ,证明:
所成的比为λ,证明:![]() ⊥(
⊥(![]() -λ
-λ![]() );
);
(2)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
|
解:(1)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程x2=4y得x2-4kx-4m=0. ① 设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根. 所以x1x2=-4m. 由点P(0,m)分有向线段 得 又点Q是点P关于原点的对称点, 故点Q的坐标是(0,-m),从而 =2m[ =2m(x1+x2)· =2m(x1+x2)· 所以 (2)由 由x2=y得y= 所以抛物线x2=4y在点A处切线的斜率为 设圆C的方程是(x-a)2+(y-b)2=r2, 则 解之得a=- 所以圆C的方程是(x+ 即x2+y2+3x-23y+72=0. |
|
注:本题第(2)问用到了导数的有关知识. |


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源:天津市新人教A版数学2012届高三单元测试35:抛物线 题型:044
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
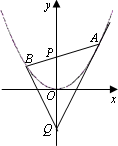
(1)设点P满足![]() =λ
=λ![]() (λ为实数),证明:
(λ为实数),证明:![]() ⊥(
⊥(![]() -λ
-λ![]() );
);
(2)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源:深圳市远恒佳教育集团龙华中英文实验学校高中部2006~2007学年度第一学期第1学段质量检测题高三数学(文) 题型:044
解答题:解答应写出文字说明,证明过程或演算步骤.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
设点P分有向线段 所成的比为λ,证明

查看答案和解析>>
科目:高中数学 来源:2007年广东高考数学模拟测试题(数学理科) 题型:044
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
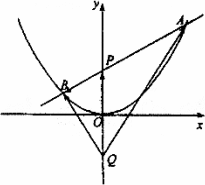
(Ⅰ)设点P分有向线段![]() 所成的比为λ,证明
所成的比为λ,证明![]() ;
;
(Ⅱ)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源:2007年广东高考数学测试题(理科) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:广东省惠州市2007届高三第一次调研考试数学试题(文科卷) 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com