
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 边上的高,沿
边上的高,沿![]() 把
把![]() 折起,使
折起,使![]() 。
。

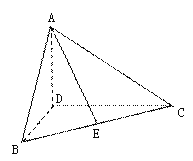
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)![]() 为
为![]() 的中点,求
的中点,求![]() 与底面
与底面![]() 所成角的正切值。
所成角的正切值。
【答案】(1)见解析;(2)![]() .
.
【解析】此题主要考查面面垂直和异面直线夹角公式的求法,第二问解题的关键是作出辅助线,此题是一道中档题,也是高考必考题;(1)已知在△ABC中,AD是BC上的高,沿AD把△ABC折起,使∠BDC=60°,可得AD⊥DC,AD⊥DB,根据面面垂直的判定定理进行求解;
(2)作辅助线,取DC中点F,连接EF,则EF∥BD,可得∠AEF为异面直线AE与BD所成的角,再根据余弦定理和向量公式进行求解;
解(Ⅰ)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,又DB![]() DC=D,
DC=D,
∴AD⊥平面BDC,∵AD 平面![]() 平面BDC.
平面BDC. ![]() 平面ABD
平面ABD![]() 平面BDC。----4分
平面BDC。----4分
(Ⅱ)由∠ BDC=![]() 及(Ⅰ)知DA,DB,DC两两垂直,不防设
及(Ⅰ)知DA,DB,DC两两垂直,不防设![]() =1,以D为坐标原点,以
=1,以D为坐标原点,以![]() 所在直线
所在直线![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
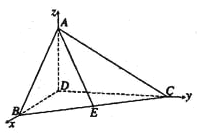
易得D(0,0,0),B(1,0,0),C(0,3,0),A(0,0, ![]() ),E(
),E(![]() ,
, ![]() ,0),
,0),
![]() =
=![]() ,
, ![]() =(1,0,0,),
=(1,0,0,),
![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为
![]() <
<![]() ,
, ![]() >=
>=
 .--------12分
.--------12分


科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
, ![]() 都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列
都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列![]() .
.
(1)设数列![]() 、
、![]() 分别为等差、等比数列,若
分别为等差、等比数列,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(2)设![]() 的首项为1,各项为正整数,
的首项为1,各项为正整数, ![]() ,若新数列
,若新数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() (
(![]() 是不小于2的正整数),
是不小于2的正整数),![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得对任意的
,使得对任意的![]() ,在
,在![]() 与
与![]() 之间数列
之间数列![]() 的项数总是
的项数总是![]() ?若存在,请给出一个满足题意的等差数列
?若存在,请给出一个满足题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤![]() )的部分图象,其图象与y轴交于点(0,
)的部分图象,其图象与y轴交于点(0,![]() )
)
(Ⅰ)求函数的解析式;
(Ⅱ)若![]() , 求
, 求![]() -
-![]() 的值.
的值.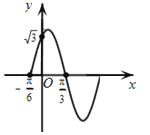
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|1﹣![]() |
|
(1)求满足f(x)=2的x值;
(2)是否存在实数a,b,且0<a<b<1,使得函数y=f(x)在区间[a,b]上的值域为[a,2b],若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
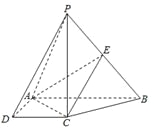
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直线PQ与⊙O切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于Q点.
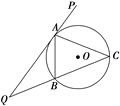
(1)求证:QC·AC=QC2-QA2;
(2)若AQ=6,AC=5,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=![]() , g(x)是二次函数,若f(g(x))的值域是[0,+∞),则函数g(x)的值域是( )
, g(x)是二次函数,若f(g(x))的值域是[0,+∞),则函数g(x)的值域是( )
A.(﹣∞,﹣1]∪[1,+∞)
B.(﹣∞,﹣1]∪[0,+∞)
C.[0,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=af(x)﹣1(a>0且a≠1).
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[﹣1,2]上的最大值;
(Ⅲ)当a=![]() 时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com