
【题目】已知函数y= ![]() +lg(﹣x2+4x﹣3)的定义域为M,
+lg(﹣x2+4x﹣3)的定义域为M,
(1)求M;
(2)当x∈M时,求函数f(x)=a2x+2+34x(a<﹣3)的最小值.
【答案】
(1)解:由题意, 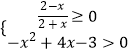 ,解得1≤x≤2,∴M=(1,2]
,解得1≤x≤2,∴M=(1,2]
(2)解:令t=2x(t∈(2,4]),f(x)=g(t)=﹣4at+3t2=3(t+ ![]() )2﹣
)2﹣ ![]()
1°﹣6<a<﹣3,即2<﹣ ![]() <4时,g(t)min=g(﹣
<4时,g(t)min=g(﹣ ![]() )=﹣
)=﹣ ![]() ;
;
2°a≤﹣6,即﹣ ![]() ≥4时,g(t)min=g(4)=48+16a
≥4时,g(t)min=g(4)=48+16a
∴f(x)min= 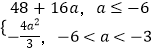
【解析】1、由题意可得,被开方数大于等于零,真数大于零。求两式的交集可得结果。
2、由整体思想令t=2x(t∈(2,4])转化可得关于t的二次函数g(t)=4at+3t2,二次函数配方可得(1)当6<a<﹣3,即2<﹣ ![]() <4时.g(t)有最小值-
<4时.g(t)有最小值-![]() .(2)a≤﹣6,即﹣
.(2)a≤﹣6,即﹣ ![]() ≥4时,g(t)min=48+16a,即得结果。
≥4时,g(t)min=48+16a,即得结果。
【考点精析】认真审题,首先需要了解复合函数单调性的判断方法(复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”),还要掌握对数函数的定义域(对数函数的定义域范围:(0,+∞))的相关知识才是答题的关键.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.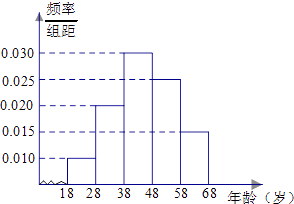
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个生物研究性学习小组,为了研究平均气温与一天内某豆类胚芽生长之间的关系,他们分别记录了4月6日至4月11日的平均气温x(℃)与该豆类胚芽一天生长的长度y(mm),得到如下数据:
日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
平均气温x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
一天生长的长度y(mm) | 22 | 25 | 29 | 26 | 16 | 12 |
该小组的研究方案是:先从这六组数据中选取6日和11日的两组数据作为检验数据,用剩下的4组数据即:7日至10日的四组数据求出线性回归方程.
(1)请按研究方案求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)用6日和11日的两组数据作为检验数据,并判断该小组所得线性回归方程是否理想.(若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm,则认为该方程是理想的)
参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接今年6月6日的“全国爱眼日”,某高中学校学生会随机抽取16名学生,经校 医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如右图,若视力测试结果不低于5.0,则称为“好视力”, 
(1)写出这组数据的众数和中位数;
(2)求从这16人中随机选取3人,至少有2人是“好视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记X表示抽到“好视力”学生的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.x,y∈R,若x+y≠0,则x≠1且y≠﹣1
B.命题“x∈R,使得x2+2x+3<0”的否定是“x∈R,都有x2+2x+3>0”
C.a∈R,“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
D.“若am2<bm2 , 则a<b”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设 ![]() ,则x+y的取值范围 .
,则x+y的取值范围 . 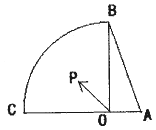
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.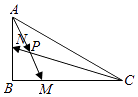
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组有9名学生.若从9名学生中选取3人,则选取的3人中恰好有一个女生的概率是 ![]() .
.
(1)该小组中男女学生各多少人?
(2)9个学生站成一列队,现要求女生保持相对顺序不变(即女生 前后顺序保持不变)重新站队,问有多少种重新站队的方法?(要求用数字作答)
(3)9名学生站成一列,要求男生必须两两站在一起,有多少种站队的方法?(要求用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com