
已知函数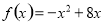 的图象上一点
的图象上一点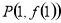 ,过
,过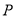 作平行于
作平行于 轴的直线
轴的直线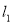 ,直线
,直线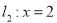 ,求函数
,求函数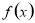 ,
, 和
和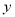 轴,及直线
轴,及直线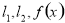 轴围成的面积
轴围成的面积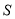
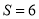
【解析】
试题分析:(1)定积分的基本思想的核心是“以直代曲”,用“有限”步骤解决“无限”问题,其方法是“分割求近似,求和取极限”,定积分只与积分区间和被积函数有关,与积分变量有关;(2)利用定积分求曲线围成图形的面积的步骤:一根据题意画简图;二确定被积函数;三确定积分的上限和下限,并求出交点坐标;四是运用微积分基本定理计算定积分,求出平面图形的面积;(3)求解时,注意要把定积分与利用定积分计算的曲线围成图形的面积区别开:定积分是一个数值,可为正,为负,也可以为零,而平面图形的面积在一般意义上总为正.
试题解析:【解析】
由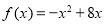 ,得
,得 . 2分
. 2分
所以阴影部分的面积
 4分
4分
 5分
5分
 8分
8分
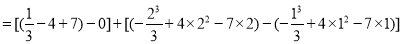
 12分.
12分.
考点:利用定积分求平面图形的面积.


科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测理科数学试卷(解析版) 题型:选择题
若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,
则此几何体的体积等于( )
A. B.
B. C.
C. D.
D.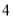
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
给出四个函数,分别满足①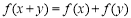 ;②
;②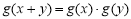 ;③
;③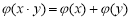 ;④
;④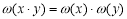 ,又给出四个函数的图象如下:
,又给出四个函数的图象如下:

则正确的配匹方案是( )
A.①—M ②—N ③—P ④—Q
B.①—N ②—P ③—M ④—Q
C.①—P ②—M ③—N ④—Q
D.①—Q ②—M ③—N ④—P
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:填空题
某班收集了50位同学的身高数据,每一个学生的性别与其身高是否高于或低于中位数的列联表如下:
| 高于中位数 | 低于中位数 | 总计 |
男 | 20 | 7 | 27 |
女 | 10 | 13 | 23 |
总计 | 30 | 20 | 50 |
为了检验性别是否与身高有关系,根据表中的数据,得到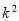 的观测值
的观测值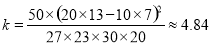 ,
,
因为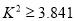 ,所以在犯错误的概率不超过 _________ 的前提下认为性别与身高有关系.
,所以在犯错误的概率不超过 _________ 的前提下认为性别与身高有关系.
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:选择题
用反证法证明命题:“若 是三连续的整数,那么
是三连续的整数,那么 中至少有一个是偶数”时,下列假设正确的是( )
中至少有一个是偶数”时,下列假设正确的是( )
A.假设 中至多有一个偶数
中至多有一个偶数
B.假设 中至多有两个偶数
中至多有两个偶数
C.假设 都是偶数
都是偶数
D.假设 都不是偶数
都不是偶数
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高三上学期第二次月考理科数学试卷(解析版) 题型:选择题
对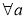 、
、 ,运算“
,运算“ ”、“
”、“ ”定义为:
”定义为: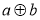 =
=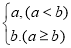 ,
,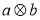 =
=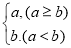 ,则下列各式其中不恒成立的是( )
,则下列各式其中不恒成立的是( )
(1)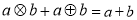 (2)
(2)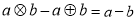
(3)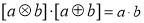 (4)
(4)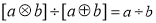
A.(1)、(3)
B.(2)、(4)
C.(1)、(2)、(3)
D.(1)、(2)、(3)、(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com