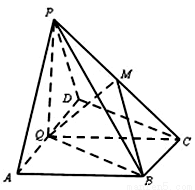
如图，在四棱锥
中，底面
为直角梯形，
，
，平面
底面
，
为
的中点，
是棱
上的点，
，
，
．
（1）求证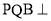：平面
平面
；
（2）若
为棱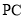
的中点，求异面直线
与
所成角的余弦值；
（3）若二面角
大小为
，求
的长．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案科目：高中数学 来源：2015-2016学年广东广州执信中学高一上学期期中数学试卷（解析版） 题型：解答题
已知函数
，
．
（1）若函数
在
上是增函数，求实数
的取值范围；
（2）若存在实数
，使得关于
的方程
有三个不相等的实数根，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源：2016届黑龙江牡丹江一中高三10月月考文数学试卷（解析版） 题型：填空题
已知
是圆心在坐标原点
的单位圆上的两点，分别位于第一象限和第四象限，且
点的纵坐标为
，
点的横坐标为
，则
．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年重庆市高一上学期期中数学试卷（解析版） 题型：解答题
集合
，
．
（1）若集合
只有一个元素，求实数
的值；
（2）若
是
的真子集，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年吉林长春十一中高一上学期期中文科数学卷（解析版） 题型：选择题
若函数的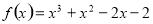
一个正数零点附近的函数值用二分法逐次计算，参考数据如下表：
|
|
|
|
|
|
那么方程
的一个近似根（精确度0．1）为（ ）
A．1．2 B．1．3 C．1．4 D．1．5
查看答案和解析>>
科目：高中数学 来源：2015-2016学年江苏省高邮市高一上学期期中调研数学试卷（解析版） 题型：解答题
已知函数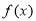
是定义在
上的奇函数，当
时，
．
（1）求函数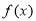的解析式；
（2）①证明函数
在
上是单调递减函数；
②判断函数在
上的单调性（不要证明）；
（3）根据你对该函数的理解，作出函数
的图像．（不需要说明理由，但要有关键特征，标出关键点）
（本题可能使用到的公式：
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则
．
、
满足：
，
，
。
，求数列｛
｝的前n项和
．
的导函数
的零点的个数；
