
【题目】
(1)求 ![]() 的值;
的值;
(2)设m , n![]() N* , n≥m , 求证:
N* , n≥m , 求证:![]() .
.
【答案】
(1)
解: ![]()
(2)
解:对任意的 ![]() ,
,
① 当 ![]() 时,左边
时,左边 ![]() ,右边
,右边 ![]() ,等式成立,
,等式成立,
② 假设 ![]() 时命题成立,
时命题成立,
即 ![]() ,
,
当 ![]() 时,
时,
左边= ![]()
![]() ,
,
右边 ![]() ,
,
而 ![]() ,
,
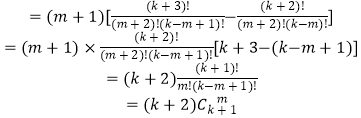
因此 ![]() ,
,
因此左边=右边,
因此 ![]() 时命题也成立,
时命题也成立,
综合①②可得命题对任意 ![]() 均成立.
均成立.
另解:因为 ![]() ,所以
,所以
左边 ![]()
![]()
又由 ![]() ,知
,知 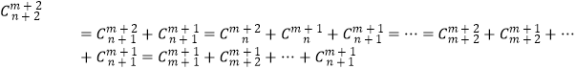 ,
,
所以,左边 ![]() 右边.
右边.
【解析】(1)由已知直接利用组合公式能求出7 ![]() 的值.(2)对任意m∈N* , 当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C
的值.(2)对任意m∈N* , 当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C ![]() +(m+2)C
+(m+2)C ![]() +(m+3)C
+(m+3)C ![]() +…+nC
+…+nC ![]() +(n+1)C
+(n+1)C ![]() =(m+1)C
=(m+1)C ![]() .
.
【考点精析】通过灵活运用组合与组合数的公式,掌握从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合即可以解答此题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n , m⊥α , n∥β , 那么α⊥β.
②如果m⊥α , n∥α , 那么m⊥n.
③如果α∥β , m ![]() α , 那么m∥β.
α , 那么m∥β.
④如果m∥n , α∥β , 那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
(1)设a=2,b= ![]() .
.
①求方程f(x)=2的根;
②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;
(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣ax﹣b,x∈R,其中a,b∈R.
(1)求f(x)的单调区间;
(2)若f(x)存在极值点x0 , 且f(x1)=f(x0),其中x1≠x0 , 求证:x1+2x0=0;
(3)设a>0,函数g(x)=|f(x)|,求证:g(x)在区间[﹣1,1]上的最大值不小于 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
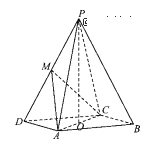
【题目】在四棱锥P-ABC中,底面ABCD为平行四边形,![]() ,O为AC的中点,
,O为AC的中点,![]() 平面
平面![]() M为PD的中点。
M为PD的中点。
(1)证明![]() 平面
平面![]() .
.
(2)证明![]() 平面
平面![]() .
.
(3)求三棱锥P-MAC体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
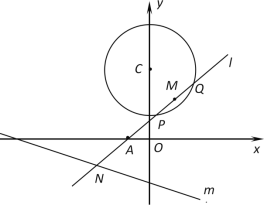
【题目】已知圆![]() :
:![]() ,一动直线l过
,一动直线l过![]() 与圆
与圆![]() 相交于
相交于![]() .两点,
.两点,![]() 是
是![]() 中点,l与直线m:
中点,l与直线m:![]() 相交于
相交于![]() .
.
(1)求证:当l与m垂直时,l必过圆心![]() ;
;
(2)当![]() 时,求直线l的方程;
时,求直线l的方程;
(3)探索![]() 是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com