
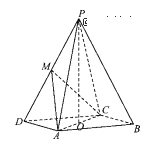
【题目】在四棱锥P-ABC中,底面ABCD为平行四边形,![]() ,O为AC的中点,
,O为AC的中点,![]() 平面
平面![]() M为PD的中点。
M为PD的中点。
(1)证明![]() 平面
平面![]() .
.
(2)证明![]() 平面
平面![]() .
.
(3)求三棱锥P-MAC体积.
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A![]() ,B
,B![]() ,锐角α的终边与单位圆O交于点P.
,锐角α的终边与单位圆O交于点P.
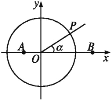
(1)用α的三角函数表示点P的坐标;
(2)当![]() =-
=-![]() 时,求α的值;
时,求α的值;
(3)在x轴上是否存在定点M,使得|![]() |=
|=![]() |恒成立?若存在,求出点M的坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x> ![]() 时,f(x+
时,f(x+ ![]() )=f(x﹣
)=f(x﹣ ![]() ).则f(6)=( )
).则f(6)=( )
A.﹣2
B.﹣1
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人,把这
个人,把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图,其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图,其中,第一组的频数为20.

(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,D是AC的中点,EF∥DB.
(1)已知AB=BC,AE=EC,求证:AC⊥FB;
(2)已知G,H分别是EC和FB的中点,求证:GH∥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知S2=4,an+1=2Sn+1,n∈N* .
(1)求通项公式an;
(2)求数列{|an﹣n﹣2|}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com