
【题目】如图,在平面直角坐标系中,点A![]() ,B
,B![]() ,锐角α的终边与单位圆O交于点P.
,锐角α的终边与单位圆O交于点P.
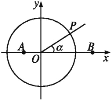
(1)用α的三角函数表示点P的坐标;
(2)当![]() =-
=-![]() 时,求α的值;
时,求α的值;
(3)在x轴上是否存在定点M,使得|![]() |=
|=![]() |恒成立?若存在,求出点M的坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)(cos α,sin α);(2)α=60°;(3)M(-2,0).
【解析】
![]() 用
用![]() 的三角函数的坐标法定义得到答案
的三角函数的坐标法定义得到答案
![]() 首先写出两个向量的坐标,根据
首先写出两个向量的坐标,根据![]() ,整理计算即可求出
,整理计算即可求出![]() 的值
的值
![]() 假设存在定点
假设存在定点![]() ,进行向量的模长运算,求得恒成立时的
,进行向量的模长运算,求得恒成立时的![]() 值
值
(1)用α的三角函数表示点P的坐标为(cos α,sin α).
(2)![]() ,
,
![]() =-
=-![]() 时,
时,
即![]() +sin2α=-
+sin2α=-![]() ,
,
整理得到cos α=![]() ,所以锐角α=60°.
,所以锐角α=60°.
(3)在x轴上假设存在定点M,设M(x,0),![]() =(cos α-x,sin α),
=(cos α-x,sin α),
则由|![]() |=
|=![]() |恒成立,得到
|恒成立,得到![]() +cos α=
+cos α=![]() (1-2xcos α+x2),整理得2(2+x)cos α=x2-4,
(1-2xcos α+x2),整理得2(2+x)cos α=x2-4,
当x=-2时等式恒成立,所以存在M(-2,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示. 
(Ⅰ)求样本中数学成绩在95分以上(含95分)的学生人数;
(Ⅱ)已知本次模拟考试全省考生的数学成绩X~N(μ,σ2),其中μ近似为样本的平均数,σ2近似为样本方差,试估计该省的所有考生中数学成绩介于100~138.2分的概率;
(Ⅲ)以频率估计概率,若从该省所有考生中随机抽取4人,记这4人中成绩在[105,125)内的人数为X,求X的分布列及数学期望.
参考数据: ![]() ≈18.9,
≈18.9, ![]() ≈19.1,
≈19.1, ![]() ≈19.4.
≈19.4.
若Z∽N(μ,σ2),则P(μ﹣σ<Z<μ+σ)=0.9826,P(μ﹣2σ<Z<μ+2σ)=0.9544,P(μ﹣3σ<Z<μ+3σ)=0.9976.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n , m⊥α , n∥β , 那么α⊥β.
②如果m⊥α , n∥α , 那么m⊥n.
③如果α∥β , m ![]() α , 那么m∥β.
α , 那么m∥β.
④如果m∥n , α∥β , 那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在长方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点.现将
上一动点.现将![]() 沿
沿![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.



图1 图2 图3
(Ⅰ)若![]() 与
与![]() 重合,且
重合,且![]() (如图2).
(如图2).
(ⅰ)证明:![]() 平面
平面![]() ;
;
(ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅱ)若![]() 不与
不与![]() 重合,且平面
重合,且平面![]() 平面
平面![]() (如图3),设
(如图3),设![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数 ![]() 图像上的点P(
图像上的点P( ![]() ,t )向左平移s(s﹥0) 个单位长度得到点P′.若 P′位于函数y=sin2x的图像上,则( )
,t )向左平移s(s﹥0) 个单位长度得到点P′.若 P′位于函数y=sin2x的图像上,则( )
A.t= ![]() ,s的最小值为
,s的最小值为 ![]()
B.t= ![]() ,s的最小值为
,s的最小值为 ![]()
C.t= ![]() ,s的最小值为
,s的最小值为 ![]()
D.t= ![]() ,s的最小值为
,s的最小值为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从含有两件正品a,b和一件次品c的3件产品中每次任取一件,连续取两次,求取出的两件产品中,恰有一件是次品的概率。
(1)每次取出不放回;(2)每次取出放回;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
(1)设a=2,b= ![]() .
.
①求方程f(x)=2的根;
②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;
(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABC中,底面ABCD为平行四边形,![]() ,O为AC的中点,
,O为AC的中点,![]() 平面
平面![]() M为PD的中点。
M为PD的中点。
(1)证明![]() 平面
平面![]() .
.
(2)证明![]() 平面
平面![]() .
.
(3)求三棱锥P-MAC体积.
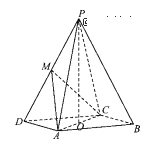
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com