
| A. | (-∞,0] | B. | (-∞,-1] | C. | [-2,0] | D. | [-1,0] |
分析 画出函数y=|f(x)|=$\left\{\begin{array}{l}{(\frac{1}{e})}^{x}-1,x≤0\\ \sqrt{2x},x>0\end{array}\right.$的图象,数形分析可得实数a的取值范围为[y′|x=0,0],求导可得答案.
解答 解:∵f(x)=$\left\{\begin{array}{l}1-{e}^{-x},x≤0\\ \sqrt{2x},x>0\end{array}\right.$,
∴函数y=|f(x)|=$\left\{\begin{array}{l}{(\frac{1}{e})}^{x}-1,x≤0\\ \sqrt{2x},x>0\end{array}\right.$的图象如下图所示:
∵y′=$\left\{\begin{array}{l}-{(\frac{1}{e})}^{x},x≤0\\ \frac{\sqrt{2x}}{2x},x>0\end{array}\right.$,
故y′|x=0=-1,
故若|f(x)|≥ax,则a∈[-1,0],
故选:D
点评 本题考查的知识点是分段函数的应用,恒成立问题,导数的几何意义,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 从甲、乙两种玉米中各抽测了10株玉米苗的高度(单位:cm),其茎叶图如图所示,根据茎叶图,下列描述正确的是( )
从甲、乙两种玉米中各抽测了10株玉米苗的高度(单位:cm),其茎叶图如图所示,根据茎叶图,下列描述正确的是( )| A. | 甲种玉米苗的平均高度大于乙种玉米苗的高度,且甲种玉米苗比乙种玉米苗长得整齐 | |
| B. | 甲种玉米苗的平均高度大于乙种玉米苗的高度,但乙种玉米苗比甲种玉米苗长得整齐 | |
| C. | 乙种玉米苗的平均高度大于甲种玉米苗的高度,且乙种玉米苗比甲种玉米苗长得整齐 | |
| D. | 乙种玉米苗的平均高度大于甲种玉米苗的高度,但甲种玉米苗比乙种玉米苗长得整齐 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
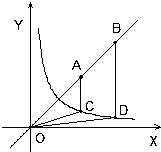 如图,点A、B为直线y=x上的两点,过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C、D两点.若BD=2AC,则4OC2-OD2的值为6.
如图,点A、B为直线y=x上的两点,过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C、D两点.若BD=2AC,则4OC2-OD2的值为6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{x\left|{x<\frac{1}{2}}\right.}\right\}$ | B. | $\left\{{x\left|{x>\frac{1}{2}}\right.}\right\}$ | C. | {x|x≥-1} | D. | {x|x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com