
 如图,圆O的直径AB=10,弦DE⊥AB于点H,BH=2.
如图,圆O的直径AB=10,弦DE⊥AB于点H,BH=2.分析 (Ⅰ)由已知中弦DE⊥AB于点H,AB为圆O的直径,由垂径定理,我们易得DH=HE,进而由相交弦定理,得DH2=AH•BH,由AB=10,HB=2,代入即可求出DH,进而得到DE的长;
(Ⅱ)由于PC切圆O于点C,由切割线定理,我们易得PC2=PD•PE,结合(Ⅰ)的结论和PC=2$\sqrt{5}$,代入即可求出PD的长.
解答 解:(Ⅰ)∵AB为圆O的直径,AB⊥DE,
∴DH=HE,
∴DH2=AH•BH=(10-2)×2=16,
∴DH=4,
∴DE=2DH=8;
(Ⅱ)∵PC切圆O于点C,
∴PC2=PD•PE,
即(2$\sqrt{5}$)2=PD•(PD+8),
∴PD=2.
点评 本题考查的知识点是垂径定理,相交弦定理及切割线定理,分析已知线段与未知线段之间的位置关系,进而选择恰当的定义进行求解是解答此类问题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
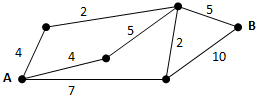 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 | a1 | a2 | a3 | a4 | a5 | a6 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com