
(14分) 如图,在三棱柱![]() 中,四边形
中,四边形![]() 是正方形,
是正方形,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 上的一点.
上的一点.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.

科目:高中数学 来源: 题型:
(本小题满分14分)
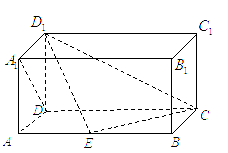 如图,在长方体
如图,在长方体![]() 中,
中,![]() ,
,![]() .
.
(1)证明:当点![]() 在棱
在棱![]() 上移动时,
上移动时,![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的平面角
的平面角
为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分) 如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
|

|
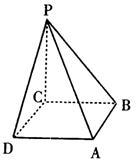
(1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(2)图3中,L、E均为棱PB上的点,且![]() ,
,![]() ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
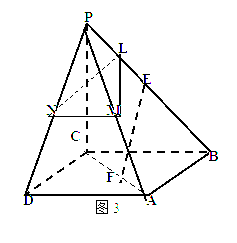
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第一次月考理科数学试卷(解析版) 题型:解答题
(本题满分14分 )如图,在三棱柱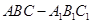 中,所有的棱长都为2,
中,所有的棱长都为2,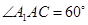 .
.
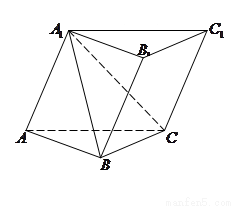
(1)求证: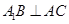 ;
;
(2)当三棱柱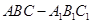 的体积最大时,
的体积最大时,
求平面 与平面
与平面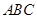 所成的锐角的余弦值.
所成的锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市丰台区高三上学期期末考试文科数学 题型:解答题
(本小题共14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.
(Ⅰ)求证:CN⊥AB1;
(Ⅱ)求证:CN //平面AB1M.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三上学期10月月考文科数学卷 题型:解答题
(本小题满分14分)
如图,在直四棱柱ABCD-A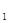 B
B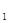 C
C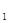 D
D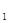 中,底面ABCD为等腰梯形,AB//CD,AB=4,
BC=CD=2,
中,底面ABCD为等腰梯形,AB//CD,AB=4,
BC=CD=2,
AA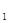 =2,
E、E
=2,
E、E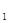 分别是棱AD、AA
分别是棱AD、AA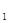 的中点.
的中点.
(1)设F是棱AB的中点,证明:直线EE //平面FCC
//平面FCC ;
;
(2)证明:平面D1AC⊥平面BB1C1C.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com