
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值及最小值.
上的最大值及最小值.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)当
.(Ⅱ)当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]() 取得最大值1.
取得最大值1.
【解析】
试题分析:(Ⅰ)先根据两角和余弦公式、二倍角公式、配角公式将函数化为基本三角函数:![]()
![]() ,再根据正弦函数性质求单调区间:由
,再根据正弦函数性质求单调区间:由![]() 解得
解得![]() ,最后写出区间形式(Ⅱ)先根据自变量范围
,最后写出区间形式(Ⅱ)先根据自变量范围![]() 确定基本三角函数定义区间:
确定基本三角函数定义区间:![]() ,再根据正弦函数在此区间图像确定最值:当
,再根据正弦函数在此区间图像确定最值:当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]() 取得最大值1.
取得最大值1.
试题解析:(Ⅰ)![]()
![]()
![]()
![]()
![]() . ……………………………………3分
. ……………………………………3分
由![]() ,
,![]() ,得
,得![]() ,
,![]() .
.
即![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() .……………………6分
.……………………6分
(Ⅱ)由![]() 得
得![]() , ………………………………8分
, ………………………………8分
所以![]() . …………………………………………10分
. …………………………………………10分
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]() 取得最大值1. ………………………………13分
取得最大值1. ………………………………13分


科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]()
![]() ,
,![]() ,其中
,其中![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求
成立?若存在,求![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为椭圆
为椭圆![]() 的长轴上的一个动点,过点
的长轴上的一个动点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都是正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求证:
,求证:![]() ;
;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若直角三角形两直角边长之和为12,求其周长![]() 的最小值;
的最小值;
(2)若三角形有一个内角为![]() ,周长为定值
,周长为定值![]() ,求面积
,求面积![]() 的最大值;
的最大值;
(3)为了研究边长![]() 满足
满足![]() 的三角形其面积是否存在最大值,现有解法如下:
的三角形其面积是否存在最大值,现有解法如下:![]() (其中
(其中![]() , 三角形面积的海伦公式),
, 三角形面积的海伦公式),
∴![]()
![]()
![]()
![]() ,
,
而![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
但是,其中等号成立的条件是![]() ,于是
,于是![]() 与
与![]() 矛盾,
矛盾,
所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
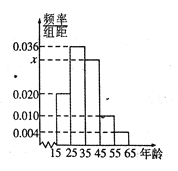
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业实行裁员增效,已知现有员工![]() 人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的
人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的![]() ,设该企业裁员
,设该企业裁员![]() 人后,年纯收益为
人后,年纯收益为![]() 万元.
万元.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出
的函数关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作一直线与抛物线
作一直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 的距离最小的点,直线
的距离最小的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.

(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com