
定义 ,
,
(Ⅰ)令函数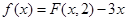 ,过坐标原点O作曲线C:
,过坐标原点O作曲线C: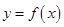 的切线
的切线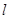 ,切点为P
,切点为P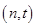 (n>0),设曲线C与
(n>0),设曲线C与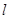 及y轴围成图形的面积为S,求S的值。
及y轴围成图形的面积为S,求S的值。
(Ⅱ)令函数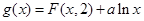 ,讨论函数
,讨论函数 是否有极值,如果有,说明是极大值还是极小值。
是否有极值,如果有,说明是极大值还是极小值。
(Ⅲ)证明:当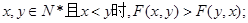
(Ⅰ)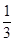 (Ⅱ)(Ⅲ)当
(Ⅱ)(Ⅲ)当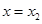 时,
时,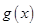 有极小值,
有极小值,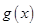 没有极大值(Ⅲ)见解析
没有极大值(Ⅲ)见解析
【解析】本试题主要是考查了导数在研究函数中的运用,以及定积分的综合运用。
(1)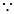
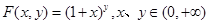 ,
,
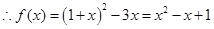 ,
,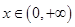 ,
,
曲线C与y轴交点为A(0,1)
又过坐标原点O向曲线C作切线,切点为P(n,t)(n>0),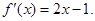
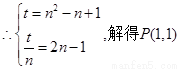 ,切线
,切线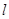 方程为
方程为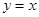
(2)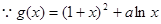 ,
,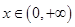 。
。
 ,
,
那么对于参数a分类讨论得到单调性得到极值。
(3)令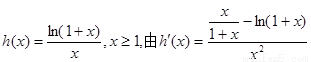
又令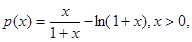
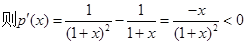
两次构造函数结合导数得到结论。解:(Ⅰ)
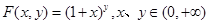 ,
,
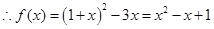 ,
,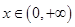 ,
,
曲线C与y轴交点为A(0,1)……………1分
又过坐标原点O向曲线C作切线,切点为P(n,t)(n>0),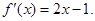
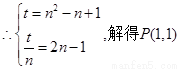 ,切线
,切线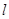 方程为
方程为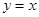 …………3分
…………3分
 ………………5分
………………5分
(Ⅱ)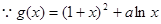 ,
,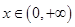 。
。
 ………………6分
………………6分
1)。当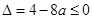 即
即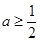 时,
时,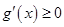 (
(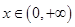 ),
),
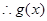 在
在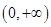 单调递增从而没有极值; ………………7分
单调递增从而没有极值; ………………7分
2)。当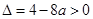 即
即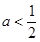 时,方程
时,方程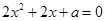 有二个不等实根
有二个不等实根
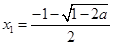 ,
,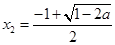 ,
,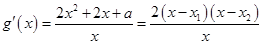
若 ,则
,则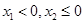 ,
,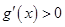 ,
,
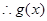 在
在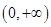 单调递增从而没有极值; ………………8分
单调递增从而没有极值; ………………8分
若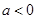 ,则
,则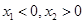 。当
。当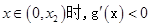 ;当
;当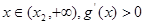
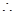 当
当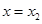 时,
时,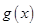 有极小值,
有极小值,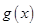 没有极大值。 ………………9分
没有极大值。 ………………9分
(Ⅲ)令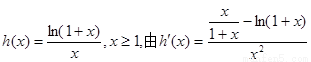 ,…………10分
,…………10分
又令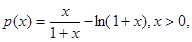
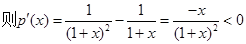 ,
,
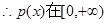 单调递减.……………………11分
单调递减.……………………11分
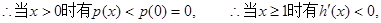
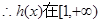 单调递减,………………12分
单调递减,………………12分
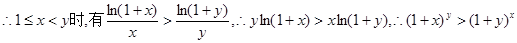 ,
,
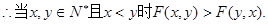 ………………14分
………………14分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
定义![]() ,
,
(1)令函数![]() 的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O作曲线C1的切线,切点为B(n,t)(n>0),设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S,求S的值。
的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O作曲线C1的切线,切点为B(n,t)(n>0),设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S,求S的值。
(2)当![]()
(3)令函数![]() 的图象为曲线C2,若存在实数b使得曲线C2在
的图象为曲线C2,若存在实数b使得曲线C2在![]() 处有斜率为-8的切线,求实数a的取值范围。
处有斜率为-8的切线,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)定义![]() ,
,
(1)令函数![]() 的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O作曲线C1的切线,切点为B(n,t)(n>0),设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S,求S的值。
的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O作曲线C1的切线,切点为B(n,t)(n>0),设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S,求S的值。
(2)当![]()
(3)令函数![]() 的图象为曲线C2,若存在实数b使得曲线C2在
的图象为曲线C2,若存在实数b使得曲线C2在![]() 处有斜率为-8的切线,求实数a的取值范围。
处有斜率为-8的切线,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010年福建省漳州一中高中毕业班质量检查(理) 题型:解答题
(本小题满分14分)
定义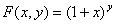 ,
,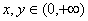 ,
,
(Ⅰ)令函数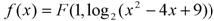 的图象为曲线
的图象为曲线 ,曲线
,曲线 与
与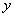 轴交于点
轴交于点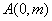 ,过坐标原点
,过坐标原点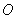 向曲线
向曲线 作切线,切点为
作切线,切点为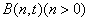 ,设曲线
,设曲线 在点
在点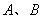 之间的曲线段与线段
之间的曲线段与线段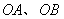 所围成图形的面积为
所围成图形的面积为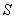 ,求
,求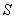 的值;
的值;
(Ⅱ)令函数 的图象为曲线
的图象为曲线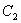 ,若存在实数
,若存在实数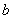 使得曲线
使得曲线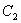 在
在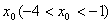 处有斜率为-8的切线,求实数
处有斜率为-8的切线,求实数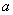 的取值范围;
的取值范围;
(Ⅲ)当 且
且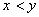 时,证明
时,证明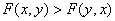 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com