
(本小题满分14分)
定义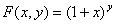 ,
,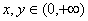 ,
,
(Ⅰ)令函数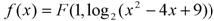 的图象为曲线
的图象为曲线 ,曲线
,曲线 与
与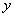 轴交于点
轴交于点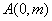 ,过坐标原点
,过坐标原点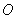 向曲线
向曲线 作切线,切点为
作切线,切点为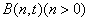 ,设曲线
,设曲线 在点
在点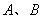 之间的曲线段与线段
之间的曲线段与线段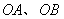 所围成图形的面积为
所围成图形的面积为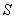 ,求
,求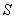 的值;
的值;
(Ⅱ)令函数 的图象为曲线
的图象为曲线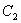 ,若存在实数
,若存在实数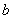 使得曲线
使得曲线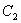 在
在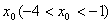 处有斜率为-8的切线,求实数
处有斜率为-8的切线,求实数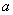 的取值范围;
的取值范围;
(Ⅲ)当 且
且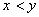 时,证明
时,证明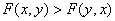 。
。
解:(Ⅰ)∵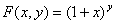
∴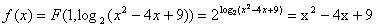 ,
,
故A(0,9), (1分)
又过坐标原点O向曲线 作切线,切点为B(n,t)
(n>0) ,
作切线,切点为B(n,t)
(n>0) ,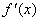 =2x-4.
=2x-4.
∴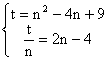 ,
,
解得B( 3,6 ) , (2分)
∴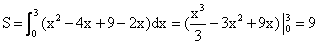 .
(4分)
.
(4分)
(Ⅱ)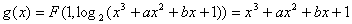 ,
,
设曲线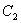 在
在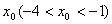 处有斜率为-8的切线,
处有斜率为-8的切线,
又由题设log2(x3+ax2+bx+1)>0 , 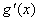 =3x2+2ax+b,
=3x2+2ax+b,
∴存在实数b使得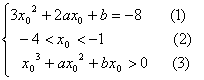 有解, (6分)
有解, (6分)
由(1)得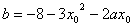 ,代入(3)得
,代入(3)得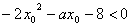 ,(7分)
,(7分)
∴由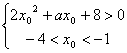 有解,
有解,
得2×(-4)2+a×(-4)+8>0或2×(-1)2+a×(-1)+8>0,
∴a<10或 , ∴
, ∴ .
(9分)
.
(9分)
(Ⅲ)令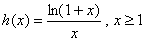 ,由
,由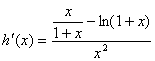 ,
(10分)
,
(10分)
又令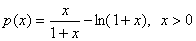 , ∴
, ∴ ,
,
∵ 在
在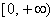 连续 ∴
连续 ∴ 在
在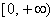 单调递减, (12分)
单调递减, (12分)
∴当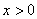 时有,
时有,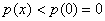 ,∴当
,∴当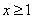 时有,
时有, ,
,
∴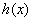 在
在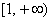 单调递减,
(13分)
单调递减,
(13分)
∴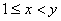 时,有
时,有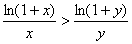 ,∴yln(1+x)>xln(1+y),
,∴yln(1+x)>xln(1+y),
∴ ,
,
∴当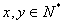 且
且 时,
时,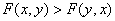 .
(14分)
.
(14分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届江西省高二第一次月考理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率;
(Ⅱ)求笼内至少剩下5只果蝇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,不等式恒成立,求实数
时,不等式恒成立,求实数![]() 的取值范围;
的取值范围;
(3)关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个相异实根,求
上恰有两个相异实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知![]() (m为常数,m>0且
(m为常数,m>0且![]() )
)
设![]() 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
(2)若bn=an·![]() ,且数列{bn}的前n项和Sn,当
,且数列{bn}的前n项和Sn,当![]() 时,求Sn;
时,求Sn;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知定点![]() 和定直线
和定直线![]() ,
,![]() 是定直线
是定直线![]() 上的两个动点且满足
上的两个动点且满足![]() ,动点
,动点![]() 满足
满足![]() ,
,![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点
两点
①求![]() 的值;
的值;
②设![]() ,当三角形
,当三角形![]() 的面积
的面积![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
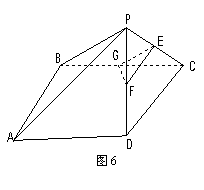 如图5,在直角梯形ABCP中,AP//BC,AP
如图5,在直角梯形ABCP中,AP//BC,AP![]() AB,AB=BC=
AB,AB=BC=![]() ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将![]() 沿CD折起,使得
沿CD折起,使得![]() 平面ABCD, 如图6.
平面ABCD, 如图6.
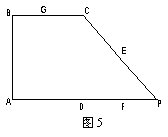 (Ⅰ)求证:AP//平面EFG;
(Ⅰ)求证:AP//平面EFG;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ)求三棱椎![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com