
分析 (1)由已知函数解析式可得an+1=2an+1,进一步得到an+1+1=2(an+1),从而可得数列{an+1}是以a1+1为首项,以2为公比的等比数列,求其通项公式后再求数列{$\frac{1}{1+{a}_{n}}$}的前n项和,代入$\frac{1}{{1+{a_1}}}+\frac{1}{{1+{a_2}}}+…+\frac{1}{{1+{a_n}}}<\frac{1}{2}$可得a1的取值范围;
(2)根据g(x)=x2+x,得bn+1=g(bn)=bn(bn+1),得到${c}_{n}=\frac{{b}_{n}}{{b}_{n+1}}$,累积可得Tk,再由bn+1=bn(bn+1),变形得到${c}_{n}=\frac{1}{{b}_{n}}-\frac{1}{{b}_{n+1}}$,求得${S}_{k}=1-\frac{1}{{b}_{k+1}}$,然后可证$\frac{T_1}{{{S_1}+{T_1}}}+\frac{T_2}{{{S_2}+{T_2}}}+…+\frac{T_n}{{{S_n}+{T_n}}}<\frac{7}{10}$.
解答 解:(1)∵f(x)=2x+1,∴an+1=f(an)=2an+1,
则an+1+1=2(an+1),即数列{an+1}是以a1+1为首项,以2为公比的等比数列,
∴${a}_{n}+1=({a}_{1}+1){2}^{n-1}$,$\frac{1}{1+{a}_{n}}=\frac{1}{{a}_{1}+1}•\frac{1}{{2}^{n-1}}$,
∴$\frac{1}{1+{a}_{1}}+\frac{1}{1+{a}_{2}}+…+\frac{1}{1+{a}_{n}}$=$\frac{1}{1+{a}_{1}}(1+\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}})$=$\frac{2-\frac{1}{{2}^{n-1}}}{1+{a}_{1}}$<$\frac{1}{2}$对任意n∈N+恒成立,
即有${a}_{1}>3-\frac{1}{{2}^{n-2}}$对任意n∈N+恒成立,故a1≥3;
(2)根据g(x)=x2+x,∴bn+1=g(bn)=bn(bn+1),
∴${c}_{n}=\frac{1}{1+{b}_{n}}=\frac{{b}_{n}}{{b}_{n+1}}$,则${T}_{n}=\frac{{b}_{1}}{{b}_{2}}•\frac{{b}_{2}}{{b}_{3}}…\frac{{b}_{n}}{{b}_{n+1}}=\frac{{b}_{1}}{{b}_{n+1}}$,
又由bn+1=bn(bn+1),得$\frac{1}{{b}_{n+1}}=\frac{1}{{b}_{n}}-\frac{1}{{b}_{n}+1}$,
∴${c}_{n}=\frac{1}{{b}_{n}}-\frac{1}{{b}_{n+1}}$,则${S}_{k}=1-\frac{1}{{b}_{k+1}}$,
∵b1=1,bk+1=bk(bk+1),∴${b}_{k+1}>{{b}_{k}}^{2}$,即有$\frac{1}{{b}_{k+1}}<\frac{1}{{{b}_{k}}^{2}}$,
又∵b1=1,b2=2,b3=6,
∴$\frac{{T}_{1}}{{S}_{1}+{T}_{1}}+\frac{{T}_{2}}{{S}_{2}+{T}_{2}}+…+\frac{{T}_{n}}{{S}_{n}+{T}_{n}}$=$\frac{1}{{b}_{2}}+\frac{1}{{b}_{3}}+…+\frac{1}{{b}_{k+1}}$$<\frac{1}{2}+\frac{1}{6}+\frac{1}{{6}^{2}}+\frac{1}{{6}^{4}}+…+\frac{1}{{6}^{2n-2}}$$<\frac{1}{2}+\frac{\frac{1}{6}}{1-\frac{1}{6}}=\frac{7}{10}$.
点评 本题考查数列与不等式的综合,考查了等比关系的确定,训练了等比数列的前n项和公式的应用,考查数学转化思想方法,属难题.


科目:高中数学 来源: 题型:选择题
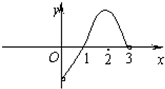 已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )
已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(x)•cosx<0的解集是( )| A. | (-3,-$\frac{π}{2}$)∪(0,1)∪($\frac{π}{2}$,3) | B. | (-3,-1)∪(-1,0)∪(0,1)∪(1,3) | ||
| C. | (-3,-$\frac{π}{2}$)∪(0,1)∪(1,3) | D. | (-3,-$\frac{π}{2}$)∪(-1,0)∪(0,1)∪($\frac{π}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | u<0 | B. | u>0 | C. | u=0 | D. | 以上都可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
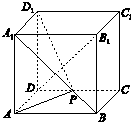 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A. | DC1⊥D1P | |
| B. | 若直线l是平面ABCD内的直线,直线m是平面DD1C1C内的直线,若l与m相交,则交点一定在直线CD上 | |
| C. | 若P为A1B上动点,则AP+PD1的最小值为$\frac{\sqrt{2}+\sqrt{6}}{2}$ | |
| D. | ∠PAD1最小为$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com