
已知圆的半径为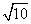 ,圆心在直线y=2x上,圆被直线x-y=0截得的弦长为4
,圆心在直线y=2x上,圆被直线x-y=0截得的弦长为4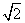 ,求圆的方程.
,求圆的方程.
解:方法一:设圆的方程是(x-a)2+(y-b)2=10.因为圆心在直线y=2x上,
所以b=2a. ①
解方程组 得2x2-2(a+b)x+a2+b2-10=0,
得2x2-2(a+b)x+a2+b2-10=0,
所以x1+x2=a+b,x1·x2= .由弦长公式得
.由弦长公式得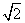 ·
· =4
=4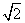 ,
,
化简得(a-b)2=4. ② 解①②组成的方程组,得a=2,b=4,
或a=-2,b=-4.故所求圆的方程是(x-2)2+(y-4)2=10,或(x+2)2+(y+4)2=10.
方法二:设圆的方程为(x-a)2+(y-b)2=10,则圆心为(a,b),半径r=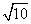 ,圆心(a,b)到直线x-y=0的距离d=
,圆心(a,b)到直线x-y=0的距离d=
由弦长、弦心距、半径组成的直角三角形得d2+( )2=r2,即
)2=r2,即 +8=10,
+8=10,
所以(a-b)2=4.又因为b=2a,所以a=2,b=4,或a=-2,b=-4.
故所求圆的方程是(x-2)2+(y-4)2=10,或(x+2)2+(y+4)2=10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如图,在长方体ABCD-A1B1C1D1中,M,N分别是棱BB1,B1C1的中点,若∠CMN=90°,则异面直线AD1和DM所成角为
A.30° B.45° 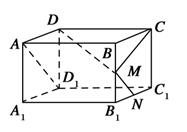 C.60° D.90°
C.60° D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com