
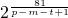 ,分析即可.
,分析即可.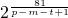 ,
,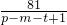 的可能取值为1,3,9,27,81,
的可能取值为1,3,9,27,81,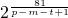 是难点,分析得到p-m-t+1必是81的正约数是关键,考查分析与运算能力,属于难题.
是难点,分析得到p-m-t+1必是81的正约数是关键,考查分析与运算能力,属于难题. 

 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
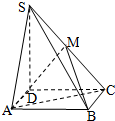 四棱锥S-ABCD中,底面ABCD为矩形,平面SDC⊥底面ABCD,AD=
四棱锥S-ABCD中,底面ABCD为矩形,平面SDC⊥底面ABCD,AD= ,DC=SD=2,
,DC=SD=2,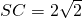 ,点M是侧棱SC的中点.(Ⅰ)求证:SD⊥平面ABCD;(Ⅱ)求二面角C-AM-B的大小.(Ⅲ)在线段BC求一点N,使点N到平面AMB的距离为
,点M是侧棱SC的中点.(Ⅰ)求证:SD⊥平面ABCD;(Ⅱ)求二面角C-AM-B的大小.(Ⅲ)在线段BC求一点N,使点N到平面AMB的距离为 .
.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| f(1)=2 | f(1.5)=0.625 | f(1.25)=-0.984 |
| f(1.375)=-0.260 | f(1.4375)=0.162 | f(1.40625)=-0.054 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
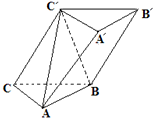 已知斜三棱柱ABC-A′B′C′每条侧棱长为3,底面为边长2的正三角形,侧面BCC′B′垂直于底面,且CC′=BC′.
已知斜三棱柱ABC-A′B′C′每条侧棱长为3,底面为边长2的正三角形,侧面BCC′B′垂直于底面,且CC′=BC′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com