
分析 设出椭圆的左焦点,关于直线y=-x的对称点P(m,n),由两直线垂直的条件:斜率之积为-1,以及中点坐标公式解得m=0,n=c,由椭圆方程可得b=c=1,进而得到a的值,再由椭圆的定义可得周长为2a+2c.
解答 解:设椭圆的左焦点为(-c,0),
点F1关于直线y=-x的对称点P(m,n),
由$\frac{n-0}{m+c}$=1,$\frac{n}{2}$=-$\frac{m-c}{2}$,解得m=0,n=c,
即P(0,c),
由题意方程可得b=c=1,a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$,
由题意的定义可得△PF1F2的周长为2a+2c=2$\sqrt{2}$+2.
故答案为:2$\sqrt{2}$+2.
点评 本题考查椭圆的定义、方程和性质,考查点关于直线对称的条件,考查运算能力,属于基础题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
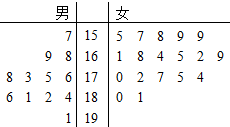 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率等于$\frac{{\sqrt{2}}}{2}$,椭圆Γ上的点到它的中心的距离的最小值为2.
已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率等于$\frac{{\sqrt{2}}}{2}$,椭圆Γ上的点到它的中心的距离的最小值为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com