练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
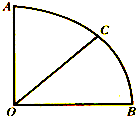
    如图，在圆心角为90°的扇形中以圆心．为起点作射线OC，则使得∠AOC与∠BOC都不大于60°的概率是（　　）
    A、
    2
    3
    B、
    1
    3
    C、
    1
    4
    D、
    3
    4
    考点：几何概型
    专题：应用题,概率与统计
    分析：本题利用几何概型求解．只须求出满足：使使得∠AOC与∠BOC都不大于60°，再将求得的角度值与整个扇形的角度求比值即得．
    解答： 解：选角度作为几何概型的测度，
    则使得∠AOC与∠BOC都不大于60°的概率是：P=
    30
    90
    =
    1
    3
    ，
    故选B．
    点评：本小题主要考查几何概型、几何概型中测度的选择等基础知识，考查运算求解能力、化归与转化思想．属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对某班级50名学生学习数学与学习物理的成绩进行调查，得到如表所示：
    数学成绩较好数学成绩一般合计
    物理成绩较好18725
    物理成绩一般61925
    合计242650
    由K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，解得K2=
    50×(18×19-6×7)2
    25×25×24×26
    ≈11.5
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    参照附表，得到的正确结论是（　　）
    A、在犯错误的概率不超过0.1%的前提下，认为“数学成绩与物理成绩有关”
    B、在犯错误的概率不超过0.1%的前提下，认为“数学成绩与物理成绩无关”
    C、有100%的把握认为“数学成绩与物理成绩有关”
    D、有99%以上的把握认为“数学成绩与物理成绩无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=x3-15x2-33x+6的单调递增区间为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数φ（x）、g（x0都是奇函数，f（x）=aφ（x）+bg（x）+2在（0，+∞）上有最大值5，则f（x）=aφ（x）+bg（x）+2在（-∞，0）上有最小值
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知k∈R，设f（θ）=cos2θ+（k-4）sinθ+2k-9，其中θ∈[0，2π）．
    （1）当k=3时，求f（θ）的最值，并求相应的θ；
    （2）若对任意θ∈[0，2π），f（θ）≤0恒成立，求k的取值范围；
    （3）若存在唯一的θ∈[0，2π），使f（θ）≤0，求θ、k的取值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，a，b，c分别为内角A，B，C的对边，且b．sin B+c•sin C=a•sinA十b•sin C
    （Ⅰ）求角A的大小；
    （Ⅱ）设函数
    m
    =（
    		3
    sin
    x
    2
    ，cos
    x
    2
    ），
    n
    =（cos
    x
    2
    ，cos
    x
    2
    ），f（x）=
    m
    .
    n
    ，当f（B）取最大值时，判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面给出四个命题的表述：
    ①直线（1+m）x+4y-3+m=0（m∈R）恒过定点（-1，1）；
    ②已知直线l：x-y+4=0与圆C：（x-1）2+（y-1）2=2，则C上各点到l的距离的最大值为3
    		2
    ；
    ③已知M={(x，y)|y=
    		1-x2
    }    ，N={（x，y）|y=x+b}，若M∩N≠Φ，
    则b∈[-
    		2
    ，
    		2
    ]；其中表述正确的是（　　）
    A、①②B、①②③C、①③D、②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若sinA：sinB：sinC=3：5：7，则这个三角形的最大内角为（　　）
    A、120°B、150°
    C、90°D、60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：x1和x2是方程x2-mx-2=0的两个实根，不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1，1]恒成立；命题q：方程a2x2+ax-2=0在[-1，1]上有解．若命题p是假命题且命题q是真命题，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案