
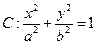 (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).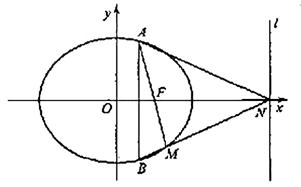
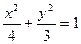 .(2)同解析
.(2)同解析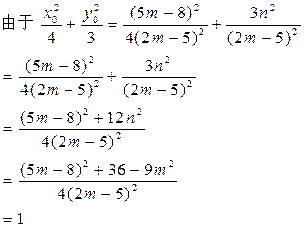
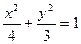 .
.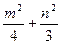 ="1." ……①
="1." ……①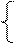 设M(x0,y0),则有 n(x0-1)-(m-1)y0="0," ……②
设M(x0,y0),则有 n(x0-1)-(m-1)y0="0," ……②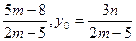 .
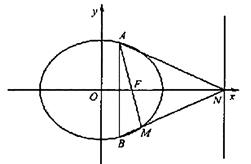
.
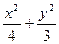 =1得(3t2+4)y2+6ty-9=0.
=1得(3t2+4)y2+6ty-9=0.
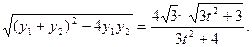
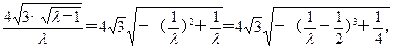
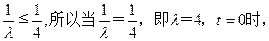
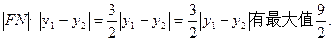
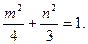 ……①
……①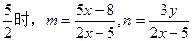 . ……④
. ……④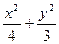 =1(y≠0).
=1(y≠0).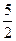 时,由②,③得:
时,由②,③得: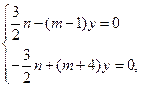
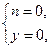 与a≠0矛盾.
与a≠0矛盾.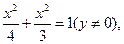 即点M恒在锥圆C上.
即点M恒在锥圆C上.

科目:高中数学 来源:不详 题型:解答题
 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于 轴上方,M为左准线上一点,
轴上方,M为左准线上一点, 为坐标原点。已知四边形
为坐标原点。已知四边形 为平行四边形,
为平行四边形, 。
。 与
与 的关系式;
的关系式;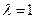 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。
,求此时的双曲线方程。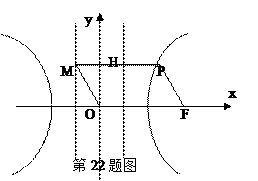
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和直线
和直线 ,过定点F与直线
,过定点F与直线 相切的动圆圆心为点C。(1)求动点C的轨迹方程; (2)过点F在直线l2交轨迹于两点P、Q,交直线l1于点R,求
相切的动圆圆心为点C。(1)求动点C的轨迹方程; (2)过点F在直线l2交轨迹于两点P、Q,交直线l1于点R,求 的最小值。
的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
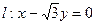 与曲线
与曲线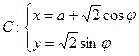
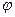 为参数,
为参数,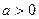 )有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .
)有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com