
| A. | -$\frac{1}{2}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{4}{5}$ |
分析 先把sin2017°转化成sin(5×360°+217°)利用诱导公式进一步化简整理求得结果为-sin37°,再根据30°<37°<45°,sin30°=$\frac{1}{2}$,sin45°=$\frac{\sqrt{2}}{2}$,而$\frac{1}{2}$<$\frac{3}{5}$<$\frac{\sqrt{2}}{2}$,答案可得.
解答 解:sin2017°=sin(5×360°+217°)=sin217°=-sin37°,
∵30°<37°<45°,sin30°=$\frac{1}{2}$,sin45°=$\frac{\sqrt{2}}{2}$,而$\frac{1}{2}$<$\frac{3}{5}$<$\frac{\sqrt{2}}{2}$,
故-sin37°≈-$\frac{3}{5}$,
故选:B.
点评 本题主要考查了三角函数的化简求值,诱导公式的应用.解题的过程中注意三角函数的正负值的判定,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| x(百元) | 5 | 6 | 7 | 8 | 9 |
| y(件) | 10 | 8 | 9 | 6 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $5\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{5\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
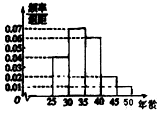 2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如图所示,并得到适龄民众对放开生育二胎政策的态度数据如表:
2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如图所示,并得到适龄民众对放开生育二胎政策的态度数据如表:| 生二胎 | 不生二胎 | 合计 | |
| 25~35岁 | 45 | 10 | 55 |
| 35~50岁 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.076 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com