
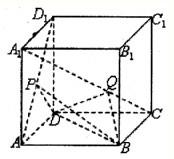
 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为AD1中点
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为AD1中点| A1Q | QC |
| A1Q |
| QC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
| A1Q |
| QC |


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

A.1个 B.2个 C.3个 D.无穷多个
查看答案和解析>>
科目:高中数学 来源: 题型:
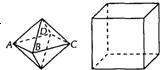
两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
(A)1个 (B)2个 (C)3个 (D)无穷多个
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省高二第二阶段考试理科数学 题型:选择题
如图2,两相同的正四棱锥组成如图所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )

A.1个 B.2个 C. 3个 D.无穷多个
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试8-理科-立体几何初步、空间向量与立体几何 题型:填空题
 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
1的正方体内,使正四棱锥的底面ABCD与正方体的某一个
平面平行,且各顶点均在正方体的面上,则这样的
几何体体积的可能值有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com