
设 均为正数,且
均为正数,且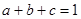
证明:(1)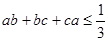 ;
;
(2)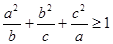 .
.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔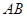 、
、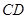 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知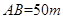 ,
,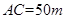 ,当
,当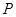 为
为 中点时,
中点时,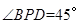 .
.
(1)求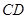 的长;
的长;
(2)试问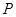 在线段
在线段 的何处时,
的何处时,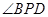 达到最大.
达到最大.
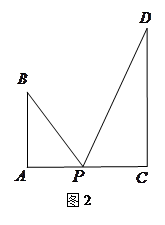
|
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某造纸厂拟建一座平面图形为矩形且面积为162m2的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/m2,中间两道隔墙建造单价为248元/m2,池底建造单价为80元/m2,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16m,试设计污水池的长和宽,使总造价最低,并求出最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
观察下列两个结论:
(Ⅰ)若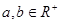 ,且
,且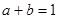 ,则
,则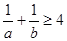 ;
;
(Ⅱ)若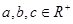 ,且
,且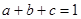 ,则
,则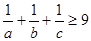 ;
;
先证明结论(Ⅱ),再类比(Ⅰ)(Ⅱ)结论,请你写出一个关于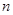 个正数
个正数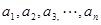 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com