
【题目】已知函数f(x)= ![]() .
.
(1)证明:f(x)+|f(x)﹣2|≥2;
(2)当x≠﹣1时,求y= ![]() 的最小值.
的最小值.
【答案】
(1)证明:因为f(x)= ![]() ≥0,
≥0,
所以f(x)+|f(x)﹣2|=|f(x)|+|2﹣f(x)|≥|f(x)+2﹣f(x)|=2,
当且仅当f(x)[2﹣f(x)]≥0即0≤f(x)≤2即﹣1﹣2 ![]() ≤x≤﹣1+2
≤x≤﹣1+2 ![]() 时取等号
时取等号
(2)解:当x≠﹣1时,f(x)= ![]() >0,
>0,
所以y= ![]() =
= ![]() +
+ ![]() +[f(x)]2≥3
+[f(x)]2≥3 ![]() =
= ![]() ,
,
当且仅当 ![]() =
= ![]() =[f(x)]2即x=﹣1±
=[f(x)]2即x=﹣1± ![]() 时取等号,
时取等号,
所以所求最小值为 ![]()
【解析】(1)通过绝对值不等式放缩可得结论;(2)通过当x≠﹣1时f(x)= ![]() >0,利用基本不等式的推广放缩可得结论.
>0,利用基本不等式的推广放缩可得结论.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


科目:高中数学 来源: 题型:
【题目】甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)求甲抽到判断题,乙抽到选择题的概率是多少;
(2)求甲、乙两人中至少有一人抽到选择题的概率是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的个数是( )
①若正实数![]() 满足
满足![]() ,则
,则![]() 的最小值是16;
的最小值是16;
②已知![]() ,则函数
,则函数![]() 的最大值为
的最大值为![]() ;
;
③已知![]() ,且
,且![]() ,则
,则![]() 的最小值是36;
的最小值是36;
④若对任意实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]() 。
。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为了保护环境,发展低碳经济,某单位在政府部门的支持下,进行技术攻关,采用了新工艺,新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似的表示为:
(吨)之间的函数关系可以近似的表示为: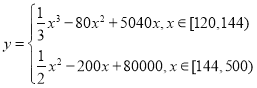 ,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
(I)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(II)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线 ![]() 的焦点,斜率为
的焦点,斜率为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() ,
, ![]() (
( ![]() )两点,且
)两点,且 ![]() .
.
(1)求该抛物线的方程;
(2)![]() 为坐标原点,
为坐标原点, ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com