Question

5．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦点为F（-c，0），F′（c，0），c＞0，过点F且平行于双曲线渐近线的直线与抛物线y²=4cx交于点P，若点P在以FF′为直径的圆上，则$\frac{{b}^{2}}{{a}^{2}}$=$\frac{\sqrt{5}-1}{2}$．

Answer 1

分析 利用抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质、联立方程组，建立a，c的关系即可得到结论．

解答 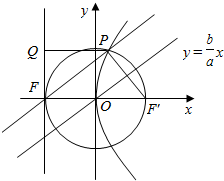解：如图，设抛物线y²=4cx的准线为l，作PQ⊥l于Q，
双曲线的右焦点为F'，由题意可知FF'为圆x²+y²=c²的直径，
∴设P（x，y），（x＞0），则PF'⊥PF，且tan∠PFF'=$\frac{b}{a}$，
∴满足$\left\{\begin{array}{l}{{y}^{2}=4cx}\\{{x}^{2}+{y}^{2}={c}^{2}}\\{\frac{y}{x+c}=\frac{b}{a}}\end{array}\right.$，
即有x²+4cx-c²=0，
则x=（-2±$\sqrt{5}$）c，
即x=（$\sqrt{5}$-2）c，或x=（-$\sqrt{5}$-2）c（舍去）
将x=（$\sqrt{5}$-2）c代入第三式，得$\frac{y}{（\sqrt{5}-1）c}$=$\frac{b}{a}$，
即y=$\frac{（\sqrt{5}-1）bc}{a}$，再将y代入第一式得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{\sqrt{5}-1}{2}$．
故答案为：$\frac{\sqrt{5}-1}{2}$．

点评 熟练掌握抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质是解题的关键．本题运算量较大，综合性较强．