
【题目】某市准备引进优秀企业进行城市建设. 城市的甲地、乙地分别对5个企业(共10个企业)进行综合评估,得分情况如茎叶图所示.

(Ⅰ)根据茎叶图,求乙地对企业评估得分的平均值和方差;
(Ⅱ)规定得分在85分以上为优秀企业. 若从甲、乙两地准备引进的优秀企业中各随机选取1个,求这两个企业得分的差的绝对值不超过5分的概率.
注:方差![]()
【答案】(Ⅰ)88,48.4.(Ⅱ)![]()
【解析】试题分析:(Ⅰ)直接利用茎叶图求解乙地对企业评估得分的平均值和方差即可.
(Ⅱ)甲区优秀企业得分为88,89,93,95共4个,乙区优秀企业得分为86,95,96共3个.列出从两个区各选一个优秀企业,所有基本事件,求出得分的绝对值的差不超过5分的个数.即可求解概率.
试题解析:(Ⅰ)乙地对企业评估得分的平均值是![]() ,
,
方差是![]() .
.
(Ⅱ)从甲、乙两地准备引进的优秀企业中各随机选取1个,有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 组, 设“得分的差的绝对值不超过5分”为事件
组, 设“得分的差的绝对值不超过5分”为事件![]() ,则事件
,则事件![]() 包含有
包含有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 组.
组.
所以![]()
所以得分的差的绝对值不超过5分的概率是![]()


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:
【题目】据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
态度 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.则获得复赛资格的人数为( )
内,其频率分布直方图如图.则获得复赛资格的人数为( )

A. 520 B. 540 C. 620 D. 640
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 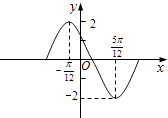
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏有这样一个环节:该关卡有一道上了锁的门,要想通过该关卡,要拿到门前密码箱里的钥匙,才能开门过关.但是密码箱需要一个密码才能打开,并且3次密码尝试错误,该密码箱被锁定,从而闯关失败.某人到达该关卡时,已经找到了可能打开密码箱的6个密码(其中只有一个能打开密码箱),他决定从中随机地选择1个密码进行尝试.若密码正确,则通关成功;否则继续尝试,直至密码箱被锁定.
(1)求这个人闯关失败的概率;
(2)设该人尝试密码的次数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABC是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE=2,点M是棱AD的中点

(I)证明:平面AED⊥平面ACD;
(Ⅱ)求锐二面角B-CM-A的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
(1)求a的值;
(2)若x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com