【题目】函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（ ）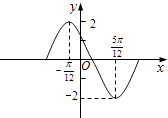 
A.y=2sin（2x+ 
）
B.y=2sin（2x+ 
）
C.y=2sin（ 
﹣ ）
D.y=2sin（2x﹣ ）
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．
（1）求证：AB∥EF；
（2）若PA=AD，且平面PAD⊥平面ABCD，求证：AF⊥平面PCD．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=xlnx，g（x）=﹣x2+ax﹣3．
（1）求函数f（x）在[t，t+2]（t＞0）上的最小值；
（2）对一切x∈（0，+∞），2f（x）≥g（x）恒成立，求实数a的取值范围．
（3）探讨函数F（x）=lnx﹣ 
+ 
是否存在零点？若存在，求出函数F（x）的零点，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某学校进行的一次语文与历史成绩中，随机抽取了25位考生的成绩进行分析，25位考生的语文成绩已经统计在茎叶图中，历史成绩如下：
（Ⅰ）请根据数据在茎叶图中完成历史成绩统计；
（Ⅱ）请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图；
语文成绩的频数分布表：
语文成绩分组 | [50，60） | [60，70） | [70，80） | [90，100） | [100，110） | [110，120] |
频数 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市准备引进优秀企业进行城市建设. 城市的甲地、乙地分别对5个企业（共10个企业）进行综合评估，得分情况如茎叶图所示.
（Ⅰ）根据茎叶图，求乙地对企业评估得分的平均值和方差；
（Ⅱ）规定得分在85分以上为优秀企业. 若从甲、乙两地准备引进的优秀企业中各随机选取1个，求这两个企业得分的差的绝对值不超过5分的概率.
注：方差
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
上一点
与椭圆右焦点的连线垂直于x轴，直线l：y＝kx＋m与椭圆C相交于A，B两点(均不在坐标轴上)．
(1)求椭圆C的标准方程；
(2)设O为坐标原点，若△AOB的面积为
，试判断直线OA与OB的斜率之积是否为定值？若是请求出，若不是请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆O：
经过点
，与x轴正半轴交于点B．
Ⅰ
______；将结果直接填写在答题卡的相应位置上
Ⅱ圆O上是否存在点P，使得
的面积为15？若存在，求出点P的坐标；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：x0∈[0，2]，log2（x+2）＜2m；命题q：关于x的方程3x2﹣2x+m2=0有两个相异实数根．
（1）若（￢p）∧q为真命题，求实数m的取值范围；
（2）若p∨q为真命题，p∧q为假命题，求实数m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
