
.将如图所示的一个直角三角形ABC(∠C=90°)绕斜边AB旋转一周,所得到的几何体的主视图是下面四个图形中的( )

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
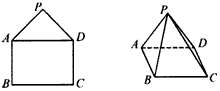
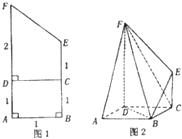 将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图2所示.
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:
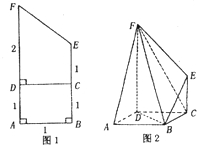 将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图2所示.
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图2所示.查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)文科数学文科数学 题型:044
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t≤100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
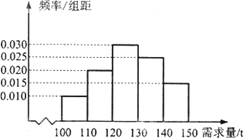
(Ⅰ)将T表示为X的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
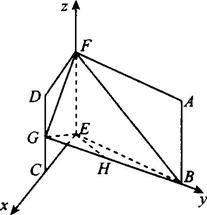
第18题图
(1)当平面BFG⊥平面BEG时,求G点的位置;
(2)在(1)的前提下,求直线GE与平面BFG所成的角.
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com